Eksponencijalne jednačine
Pre rešavanja eksponencijalne jednačine podsetimo se osobina stepena:
- dva stepena jednakih osnova jednaki su ako su im jednaki izložioci,
- dva stepena različitih osnova jednaki su ako su im izložioci jednaki jedinici,
- stepen bilo koje osnove jednak je jedinici ako mu je izložilac 0,
- stepen čiji je izložilac negativan broj, prelazi u recipročnu vrednost a izloćilac menja znak.
Neki tipovi eksponencijalnih jednačine
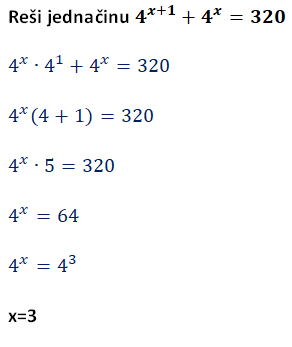
Eksponencijalna definisana je definisana za ∀x∈R
Suprotan smer pravila :ako se stepeni istih osnova množe izložioci se sabiraju
Zajednički faktor zapisan ispred zagrade
Ako u zagradi ostaje konstanta imamo mogućnost da stepen bude sam sa leve strane
Levu i desnu stranu svodimo na stepene istih osnova
Dva stepena su jednaka ako su im jednake osnove i ako su im jednaki izložioci
Rešenje eksponencijalne jednačine
U jednačini imamo stepene različitih osnova.
Sređujemo stepen sa osnovom 2 sa leve strane i osnovom 3 sa desne
Jednačinu delimo sa 3x(3/8) . sa leve strane imamo deljenje stepena istih izložilaca a sa desne konstantu.
Levu i desnu stranu svodimo na stepene istih osnova
Rešenje eksponencijalne jednačine
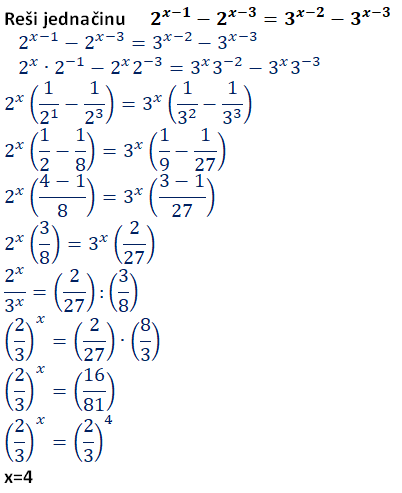
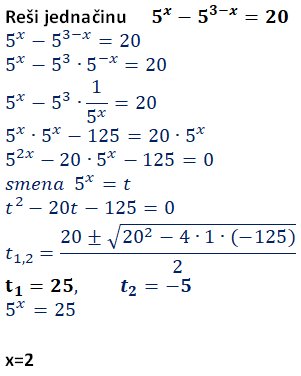
Za stepena 5x i 5-x ili 52x i 5x rastavljanje na proste činioce ne daje proizvod stepena sa promenljivom u izložiocu i konstante. Ako sredićemo jednačinu i uvedemo smenu dobijamo kvadratnu jednačinu
Rešavamo jednačinu po t i analiziramo rešenja.
t1 prihvatamo jer veće od 0, a t2 odbacujemo jer vrednost stepena 5x ne može biti negativan broj .
Prihvaćeno rešenje vraćamo u smenu i dobijamo vrednost nezavisno promenljive
Rešenje eksponencijalne jednačine

U zadatku su data tri stepena različitih osnova. Analiziramo osnove 20, 5 i 10. Brojeve 20 i 10 možemo zapisati proizvod 4=22 i 5 odnosno 2 i 5. To nam daje mogućnost da jednačinu podelimo sa 5x (uvek različito od 0) i jednačinu svedemo na kvadratnu.
Zadatak možete rešiti i ako delite stepenom 10x.
Rešenje eksponencijalne jednačine:

