Logaritamska funkcija, je inverzna funkcija eksponencijalne funkcije .
Za eksponencijalnu funkciju znamo da je definisana za ∀x∈R, i da ima pozitivne vrednosti y>0.
Njena inverzna funkcija mora da ima oblast definisanosti x>0 i skup vrednosti funkcije ∀y∈R. Dakle za logaritamsku funkciju možemo reći je definisana samo za poyitivne vrednosti x i da na svom toku menja znak . Kao posledica promene znaka javlja se nula fukcije – presek sa x-osom.
Kako esponencijalna funkcija menja monotonost u zavisnosti od vrednosti osnove to i za logaritamsku očekujemo promene monotonosti.
Logaritamsku funkciju možemo nacrtati tako što najpre nacrtamo grafik eksponencijalne funkcije a zatim je preslikamo osnom simetrijom u odnosu na pravu y=x.
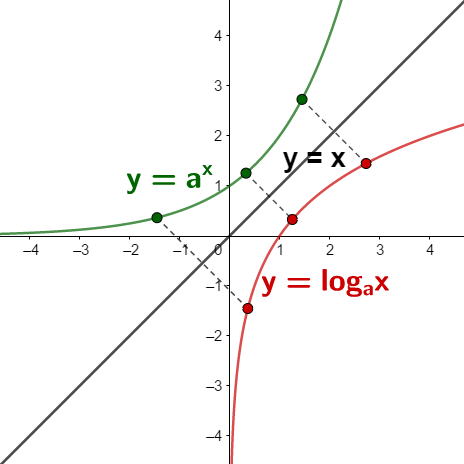
y=ax eksponencijalna funkcija
y=logax logaritamska funkcija
y=x osa simetrije
Logaritamska funkcija – aplet
Promenu monotonosti logaritamske funkcije možete videti u interaktivnom apletu ako za osnovu logaritma birate brojeve iz intervala (0,1) ili a>1 umesto unete vrednosti 0.2.
Opšte osobine logaritamske funkcije y=logax
oblast definisanosti x>0, a>0, a≠1, presek sa x-osom N(1,0)- nula funkcije, presek sa y osom nema, menja znak u tački N, nema ekstremnih vrednosti.
Ako je a>1 funkcija raste, ako je iz intervala (0,1) funkcija opada.
Sledi strana sa složenijim logaritamskim funkcijama sa njihovim grafikom i tokom
