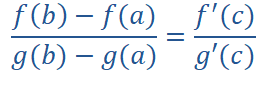Definisaćemo prvi izvod funkcije:
Ако је funkcija f(x) definisana на intervalu (a,b) i da je tačka x0 ∈(a,b) fiksna tačka.
Uočimo neku proizvoljnu tačku x ∈(a,b) . Razlika x1 – x0 pokazuje promenu ili priraštaj vrednosti nezavisno promenljive x i obeležava sa ∆ x = x – x0
Razlika f(x)- f(x0) predstavlja odgovarajuću promenu ili priraštaj funkcije f(x) i obično se obeležava sa
∆ f(x)= f(x )- f(x0 ) ili ako je funkcija označena sa y=f(x) može se zapisati: ∆ y= f(x)- f(x0 ).
Definicija: Prvi izvod funkcije y=f(x) , f:(a,b)→R, u tački x0 ∈(a,b) dat je formulom
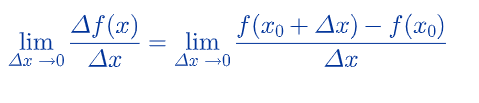
Izvod funkcije jednak je graničnoj vrednosti količnika priraštaja funkcije i priraštaja nezavisno promenljive, kad priraštaj nezavisno promenljive teži nuli.

Osnovne teoreme diferencijalnog računa
Fermaova teorema: Neka je funkcija y=f(x) definisana na odsečku [a,b] i neka u nekoj tački c∈(a,b) ima najveću (ili najmanju) vrednost. Ako postoji obostrani konačan izvod f′(c) , onda je f′(c) = 0.
Darbuova teorema: Ako funkcija y=f(x) ima konačan izvod u svakoj tački odsečka [a,b] , tada funkcija y′=f′(x) za x∈[a,b] uzima bar jednom sve vrednosti izmeñu f′(a) i f ′(b) .
Rolova teorema: Neka je funkcija y=f(x) definisana i neprekidna na odsečku [a,b] i neka postoji konačan izvod y′=f′(x) bar na intervalu (a,b) i neka je f(a) = f(b). Tada postoji bar jedan broj c∈(a,b) , takaKošijeva teorema da je f′(c) = 0.
Lagranžova teorema: Neka je funkcija y=f(x) definisana i neprekidna na odsečku [a,b] i neka postoji konačan izvod y′=f′(x) bar u svakoj tački na intervalu (a,b) . Tada postoji bar jedan broj c∈(a,b) , takav da je :
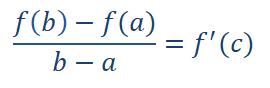
Košijeva teorema: Neka su funkcije f(x) i g(x) definisane i neprekidne na odsečku [a,b] , neka postoje konačni izvodi f′(x) i g′(x) bar na intervalu (a,b) i neka je g′(x) ≠0, za svako x∈(a,b). Tada postoji bar jedan broj c∈(a,b) takav da je :