Елипса је скуп тачака у равни са особином да је збир растојања сваке тачке тог скупа од две стална тачке константан. Те сталне тачке су жиже или фокуси елипсе. Ако је растојање између жижа 2c, а збир растојања тачке M(x, y) од фокуса једнак 2а, онда је једначина елипсе
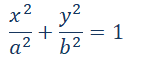
при чему је b2=a2-c2.
Kанонски облик централне једначине елипсе може се записати :
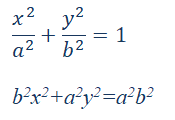
Елипса је уписана у правоугаоник чије су дужине страница 2а и 2b. Тачке у којима елипса сече осе су темена елипсе
F1(-c,0),F2(c,0) – жиже (фокуси) елипсе
2a– велика оса (а је велика полуоса) елипсе
2b- мала оса (b мала полуоса) елипсе
r1=F1M, r2=F2M, -потези ( радијус вектори) r1+r2=2a,
c2=a2-b2– линеарни ексцентрицитет
e=c/a – нумерички ексцентрицитет
Елипса може да се нацрта тако што се узме конац дужине 2а, карајеви конца се фиксирају на растојању 2c, оловком се затегне канап и црта линија. Координатни систем се постави тако да x оса пролази кроз фиксиране тачке F1 и F2, а y оса је симетрала дужи F1F2
Пример 1.
Одредити једначину елипсе ако се два њена темена налазе у тачкама А(-9,0) и В(9,0), а једна жижа има координате F1(-6,0).
На основу координате тачака А и В следи да су А и В темена елипсе на х оси, тј,
а=9, c=6
b2=a2-c2=81-36=45
Једначина елипсе је
Права и елипса
Нека је елипса дата једначином b2x2+a2y2=a2b2 а права l:y=kx+n
Решићемо систем:
b2x2+a2 (kx+n)2=a2b2
b2x2+a2(k2x2+2kxn+n2)=a2b2
b2x2+a2k2x2+2 a2kxn+ a2n2-a2b2=0
x2(b2+a2k2)+2 a2kxn+ a2n2-a2b2=0
D=4a4 k2 n2 -4(b2 +a2 k2)(a2 n2 –a2 b2 )
D=4a4k2n2-4(a2b2n2+a4k2n2-a2b4-a4b2k2)
D=a4k2n2-a2b2n2-a4k2n2+a2b4+a4b2k2
D=a2b2(-n2+b2+a2k2)
D=a2b2(a2k2+b2-n2)
Ако је D>0 једначина, тј. систем има два реална и различита решења, а то значи да права сече елипсу. Ако је D<0 једначина нема реалних решења, па права нема заједничких тачака са елипсом. Ако је D=0 тада једначина има двоструко решење, тј. једно решење и права додирује елипсу.
k2a2+b2-n2> – права сече елипсу;
k2a2+b2-n2< – права нема заједничких тачака са елипсом и
k2a2+b2-n2= – права додирује елипсу.
Услов додира праве и елипсе се може записати у облику
k2a2+b2=n2
Ако тачка M(x0,y0) припада елипси онда је једначина тангенте кроз ту тачку xx0/a2+yy0/b2=1
Povratak na stranu Analitička geometrija
