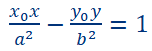Hiperbola
Hiperbola je skup tačaka u ravni sa osobinom da je razlika rastojanja svake tačke tog skupa od dve stalna tačke konstantan. Te stalne tačke su žiže ili fokusi hiperbole. Ako je rastojanje između žiža 2c, a razlika rastojanja tačke M(x, y) od fokusa jednak 2a, onda je jednačina hiperbole
pri čemu je b2=c2-a2.
Ovo je kanonski oblik centralne jednačine hiperbole. Jednačina se može zapisati i na sledeći način
b2x2-a2y2=a2b2
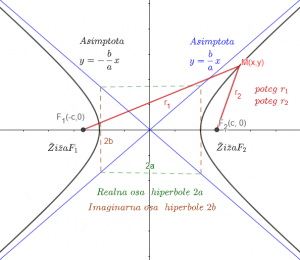
Tačke u kojima hiperbola seče x osu su temena..
Ι F1M-F2M Ι=Ι r1-r2 Ι=2a
2a-dužina realne ose hiperbole
2b– dužina imaginarne ose hiperbole
F1(-c,0), F2(c,0) – žiže (fokusi) hiperbole
linearni ekscentricitet hiperbole
numerički ekscentricitet hiperbole
, 
jednačine asimptota hiperbole
Asimptote hiperbole su prave određene dijagonalama pravougaonika čije su stranice 2a i 2b.
Prava i hiperbola
Neka je hiperbola data jednačinom
a prava l: y=kx+n
Rešavanjem sistema te dve jednačine dobijaju se veze izmeću prave i hiperbole
a2k2-b2-n2<0- prava seče hiperbolu;
a2k2-b2-n2>0 – prava nema zajedničkih tačaka sa hiperbolom i
a2k2-b2-n2=0 – prava dodiruje hiperbolu.
Uslov dodira prave i hiperbole se može zapisati u obliku a2k2-b2=n2
Ako tačka M(x0,y0) pripada hiperboli onda je jednačina tangente kroz tu tačku
