Neka je O fiksirana tačka ravni π i k dati broj različit od nule. Homotetija ravni π sa centrom u O i koeficijentom k, je preslikavanje Ho,k:π→π koje svakoj taki X ravni π dodeljuje taku X1 iste ravni takvu da je ![]()
Homotetija duž preskikava u duž, paralelne prave u paralelne, ugao u ugao.
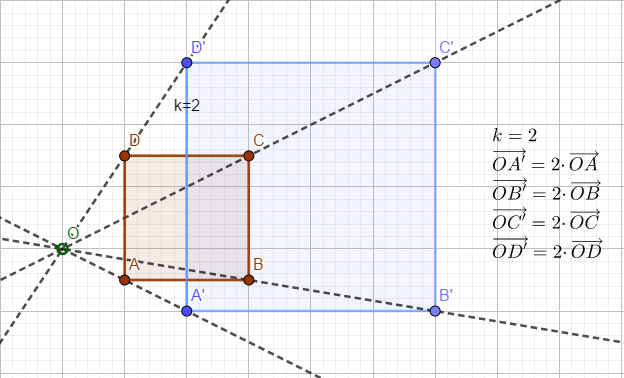
Koeficijent proporcionalnosti može biti pozitivan ili negativan. Na slikama koje slede data je najpre homotetija sa pozitivnim a zatim sa negativnim koeficijentom.
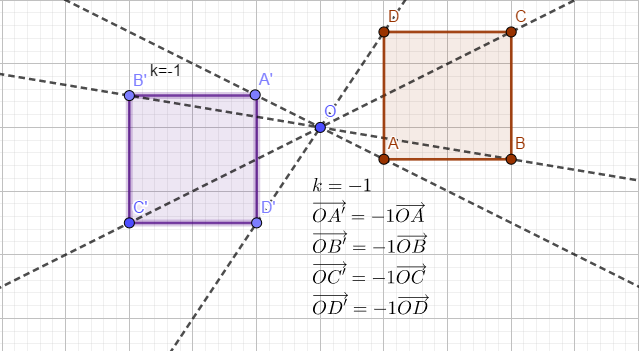
Kvadrat ABCD preslikan je u kvadrat A’B’C’D’ homotetijom sa koeficijentom k=-1 i centrom u tački O.
Figure se ne nalaze sa iste strane tačke O.
Kvadrat ABCD preslikan je u kvadrat A’B’C’D’ homotetijom sa koeficijentom k=2 i centrom u tački O.
Figure se nalaze sa iste strane tačke O.