‌

Osna simetrija

Definicija:

Preslikavanje ravni, pri kojem se svaka tačka A te ravni preslikava u tačku A’ , simetričnu sa A u odnosu na pravu s  te ravni, nazivamo osnom simetrijom u odnosu na pravu ( osu ) s. Najčešća oznaka za osnu simetriju je Ss ili Is.

Za dve figure F i F’ neke ravni kažemo da su osno simetrične u odnosu na pravu s te ravni  , ako svakoj tački X figure F odgovara tačka X’ figure F’ , tako da je S s (X ) = X’ . Naravno, važi i obrnuto, svakoj tački Q’ figure F’ odgovara tačka Q figure F tako da je    Ss ( Q ) = Q’. Osna simetrija je izometrija sa osobinama :

  • Osna simetrija je indirektna izometrijska transformacija.
  • Osnom simetrijom se sve tačke ose preslikavaju u sebe. Važi i obrnuto, ako osna simetrija preslikava neku tačku u sebe onda se tačka nalazi na osi
  • Osnom simetrijom se svaka prava normalna na osu preslikava u sebe
  • Ako je Ss(X)=X’ tada je i Ss(X’)=X
  • Ako je Ss(F)=F’ tada je i Ss(F’)=F
  • Osno simetrične figure su podudarne

 

 

  •  
osna simetrija

 

 

 

Osna simetrija

Centralna simetrija

Neka je S fiksirana tačka u ravni. Uočimo proizvoljnu tačku x različitu od S . Tada postoji jedinstvena tačka X’ takva da je X-S-X’ i XS≅SX’.

Za tačke X i X’ kažemo da su simetrične u odnosu na tačku S. Tačka S je centar simetrije.

Još se može reći i da je tačka X simetrična sa tačkom X’ u odnosu na tačku S, odnosno da je X’ simetrična sa X u odnosu na S.

Definicija:

Preslikavanje koje svaku tačku A neke ravni α prevodi u tačku A’ koja je simetrična sa tačkom A u odnosu na tačku S te ravni α , naziva se centralna simetrija ravni α sa centrom u S.

Centralna simetrija se najčešće obeležava sa SS  ili IS

Definicija:

Za figuru F ravni α kažemo da se preslikava na figuru F’ centralnom simetrijom SS  ako svakoj tački A figure F odgovara tačka A’ figure F’ koja je centralno simetrična tački A: A’=SS (A) i obrnuto.

Za centralnu simetriju možemo reći da ima sledeće osobine:

  • Centralna  simetrija je indirektna izometrijska transformacija.
  • Centralna  simetrija preslikava jedino cetar simetrije u sebe. Važi i obrnuto, ako centralna  simetrija preslikava neku tačku u sebe onda je to centar simetrije .
  • Prave koje sadrže centar simetrije preslikavaju se u sebe
  • Ako je Ss(X)=X’ tada je i Ss(X’)=X
  • Ako je Ss(F)=F’ tada je i Ss(F’)=F

 

 

 

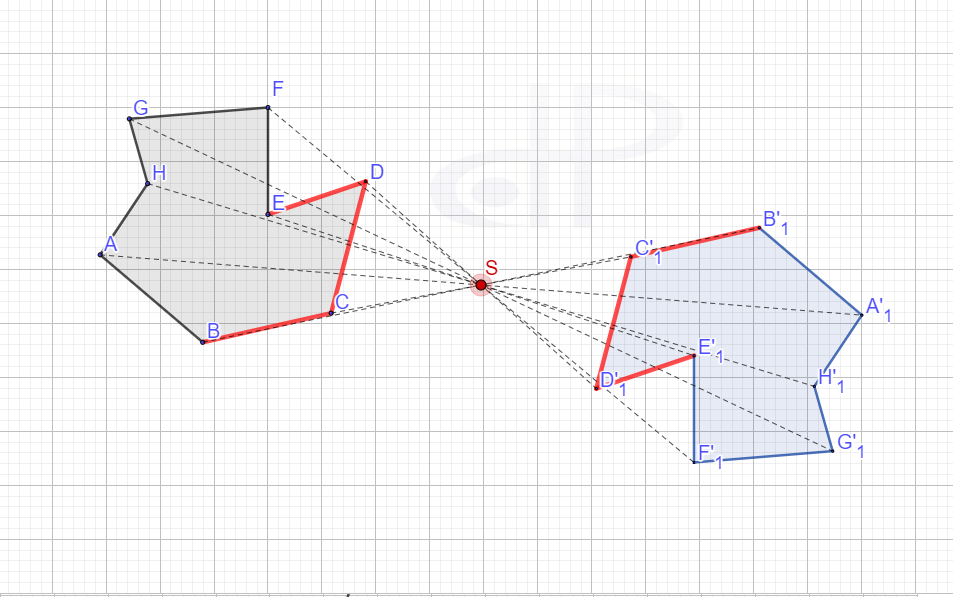
Centralna simetrija sa centrom S

centralna simetrija

Rotacija

Neka je O fiksirana tačka ravni  π i α orijentisani ugao ravni. Uočimo proizvoljnu tačku X ravni različitu od O. Postaji jedinstvena taka X’ takva da je OX≅OX’ i ugao XOX’ , orijentisani ugao α. Kažemo da je tačka X’ dobijena rotacijom tačke X oko tačke O za orijentisani ugao α

Neka je O fiksirana tačka ravni  π i α orijentisani ugao ravni. Rotacija ravni  π oko tačke O za orijentisani ugao α je preslikavanjr Ro,α: π→ π koje svakoj tačke X ravni π dodeljuje tačku X’ iste ravni koja je dobijena rotacijom oko tačke O za orijentisani ugao α. Tačka O se naziva cetar rotacije , a α ugao rotacije.

Rotacija je izometrija sa osobinama :

  • Rotacija je direktna izometrijska transformacija
  • Jedina tačka koja se rotacijom preslikava u sebe je centar rotacije.
  • Rotacija za opružen ugao je centralna simetrija . Rotacija za pun ugao je koincidencija
  • Ako je Ro,α (X)=X’ , onda je rotacija Ro,-α(X’)=X
rotacija

 

 

Rotacija okotačke O za 121.09°

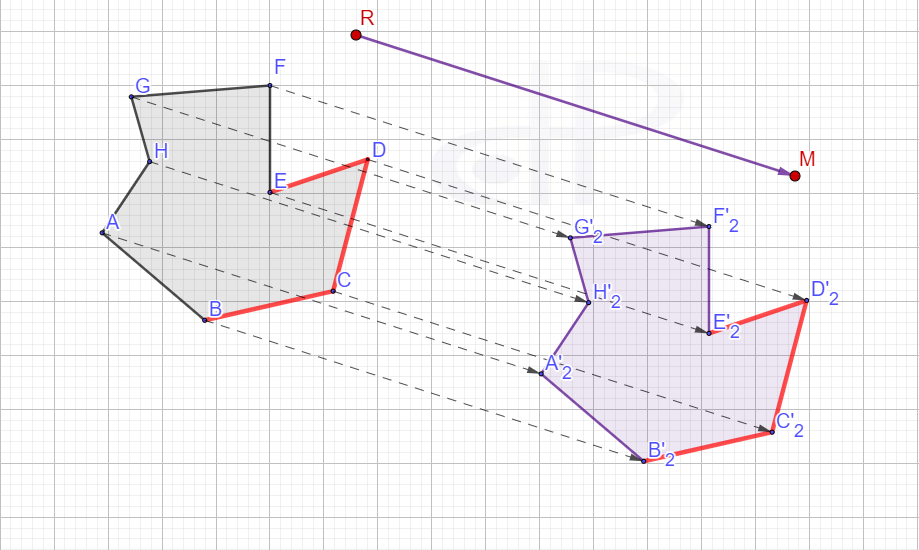
 Translacija

Neka jeVektordati vektor koji nije nula vektor i čiji je pravac paralelan sa ravni pi. Uočimo proizvoljnu tačku X ravni. Tada, postoji jedinsvena tačka X’ takva da je vektor XX’≅Vektor . Kažemo da je tačka X’ dobijena translacijom tačke X za vektor Vektor.

Definicija:

Neka je  Vektor dati vektor čiji je pravac paralelen sa ravni π. Translacija ravni π za vektor Vektor je preslikavanje     T:π→π, koje svakoj tački X ravni dodeljuje tačku X’ iste ravni koja je dobijena translacijom za vektor Vektor

Translacija je izometrijsa sa sledećim osobinama:

  • Translacija je direktna izometrijska transformacija
  • Ne postoji tačka koja se translacijom preslikava u sebe
  • Svaka prava šparalelna vektoru translacije preslikava se u sebe.
  • Translacijom se prava preslikava u paralelnu pravu.
  • Ako  T(X)=X’ tada je  T(X’)=X

 

 

Translacija figure za vektor Vektor

translacija

Povratak na stranu Planimetrija

Izometrije osna simetrija, centralna simetrija, translacija, rotacija definicije osnovne konstrukcije i konstruktivni zadaci