Krug
Krug
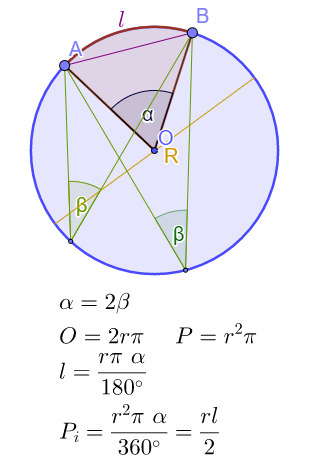
Tetiva je duž koja spaja dve tačke na kružnici. Najveća tetiva je prečnik kruga.
Centralni ugao ima teme u centru kružnice, a periferijski ima teme na kružnici. Odnos centralnog i periferijskog ugla nad istom tetivom je 1:2 . Periferijski ugao nad prečnikom prav ugao. Svi periferijski uglovi određeni istom tetivom su jednaki ako su sa iste strane tetive. Ako nisu sa iste strane njihov zbir je 180°.
Trougao
Oznake
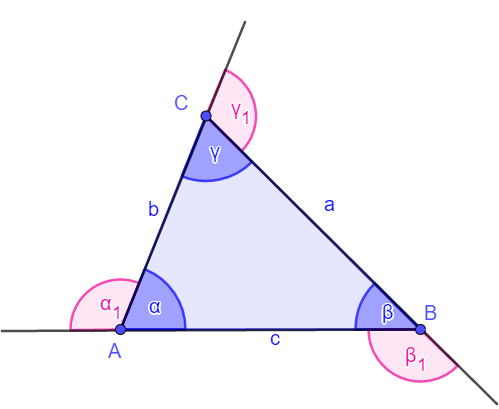
Temena geometrijskih figura obeležavamo velikim latiničnim slovima A, B, C, …,
stranice malim latiničnim slovima a, b, c, …
unutrašnje uglove α, β, γ, …
spoljašnje uglove sa α1, β1, γ1, …
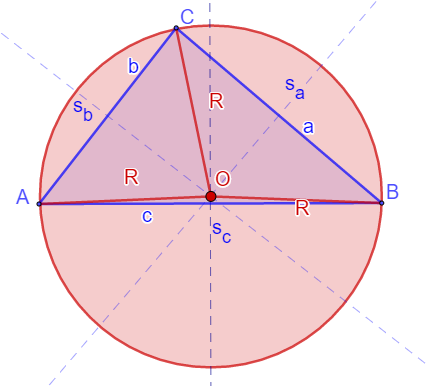
Centar upisane kružnice
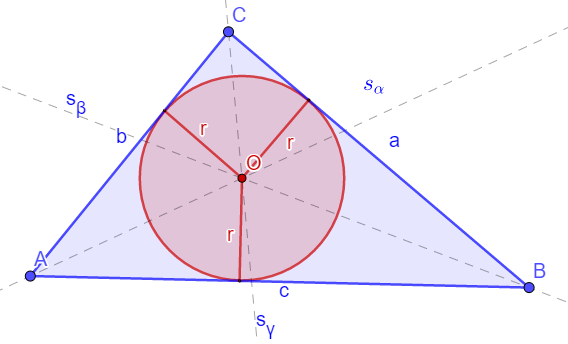
Simetrala ugla trougla je prava koja polovi unutrašnji ugao trougla. Simetrale obeležavamo sa sα, sβ, sγ . Simetrale se seku u jednoj tački.
Presek simetrala uglova je centar upisane kružnice.
Centar opisane kružnice
Simetrala stranice trogla je prava koja je normalna na stranicu trougla i sadrži stredište te stranice. Simetrale stranica trougla se seku u jednoj tački.
Simetrale stranica obeležavamo sa sa, sb, sc ili ma, mb, mc
Presek simetrala stranica je centar opisane kružnice.
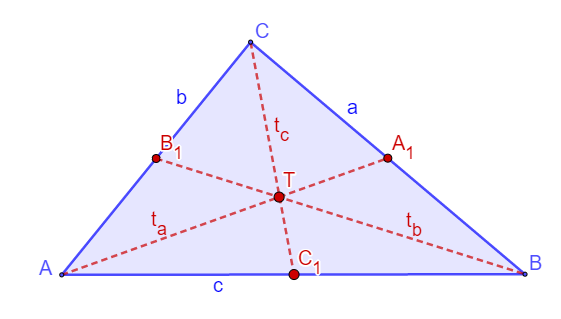
Težište trougla
Težišna duž trougla je duž određena temenom trougla i sredinom naspramne stranice. Težišne duži trougla se seku u jednoj tački.
Težišne duži obeležavamo sa ta, tb, tc .
Tačka T je težište trougla i deli svaku težišnu duž u odnosu 2:1.
Ortocentar
Visina trougla je duž određena temenom trougla i podnožijem normale spuštene iz tog temena na naspramnu stranicu trougla. Visine trougla se seku u jednoj tački. Tu tačku obeležavamo sa H.
Visine obeležavamo sa ha, hb, hc .
Tu tačku označavamo sa H i zovamo ortocentar.
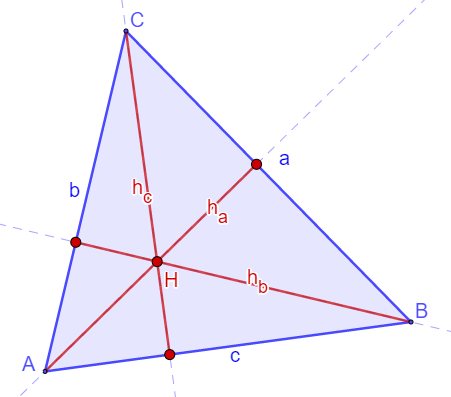
Za sve trouglove važe formule :

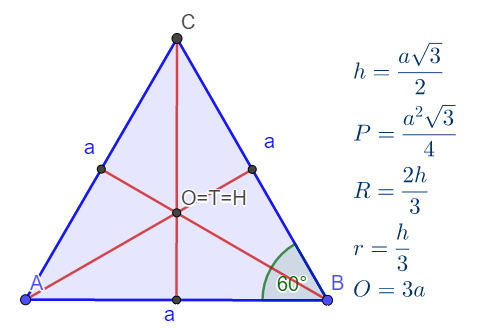
Jednakostraničan trougao
Ima jednke stranice, jednake unutrašne uglove 60° i jednake spoljašnje uglove 120°.
Sve značajne tačke trouga se poklapaju. Visina i težišna duž odgovarajuće stranice leže na simetrali ugla tj simetrali stranice.
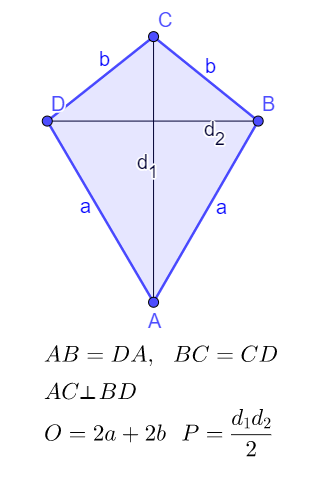
Četvorougao
Zbir unutrašnjih uglova četvorougla α+β+γ+δ=360º. Zbir spoljašnjih uglova četvorougla α1+β1+γ1+δ1=360º.
O = a +b +c +d
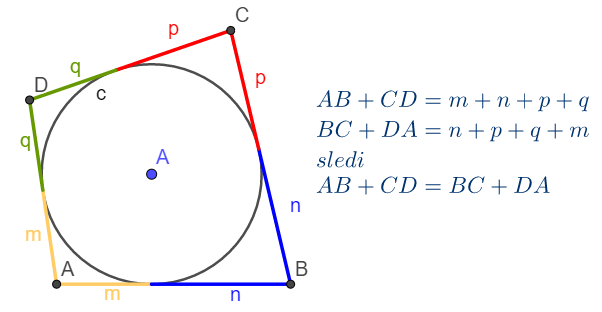
Tangentni četvorougao
U četvorougao se može upisati kružnica ako je a + c = b + d. Takav četvorougao naziva se tangentni četvorougao.
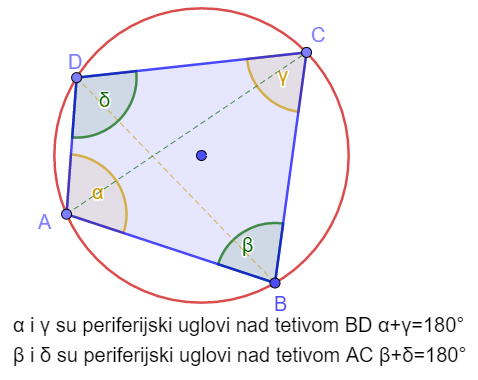
Tetivni četvorougao
Ako se oko četvorougla se može opisati kružnica tada važi α +γ = β+δ i takav četvorougao naziva se tetivni.
Paralelogram
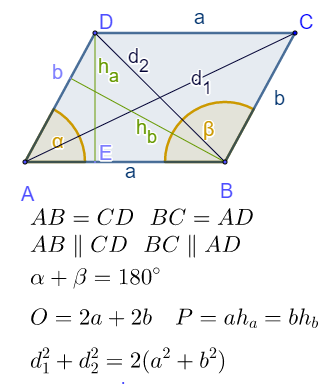
Paralelogram je četvorougao kod koga su naspramne stranice jednake i paralelne.
Uglovi na jednoj stranici su suplementni
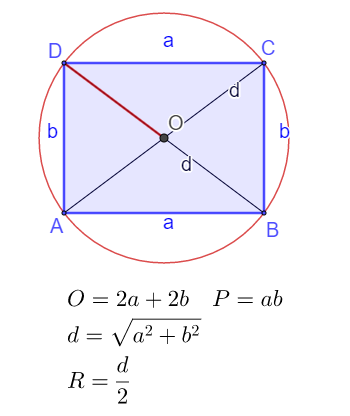
Pravougaonik
Paralelogram čiji su uglovi pravi je pravougaonik. On ima jednake dijagonale i oko njega se može opisati kružnica jer je zbir naspramnih uglova 180° tj. pravougaonik je tetivni četvorougao.
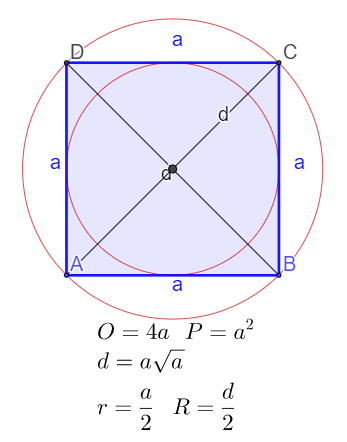
Kvadrat
Kvadrat je pravougaonik kod koga su sve stranice jednake. Dijagonale su jednake i seku se pod pravim uglom. U kvadrat se može upisati i oko njega opisati kružnica.
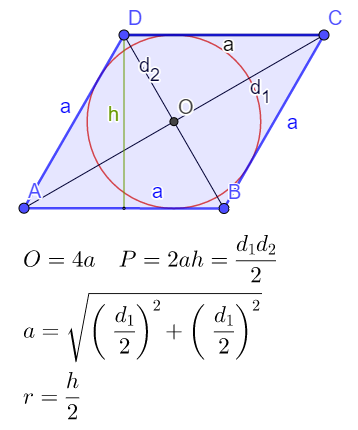
Romb
Romb je paralelogram koji ima sve stranice jednake. Kod romba se dijagonale polove i seku se pod pravim uglom (d1 ⊥d2 )
.
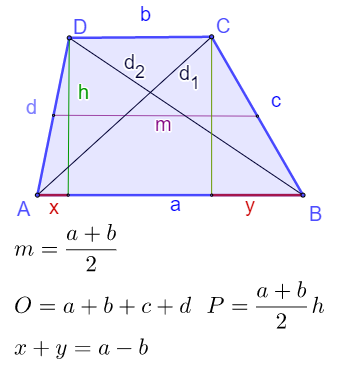
Trapez
Trapez je četvorougao koji ima jedan par pralelnih (osnovice a i b) i stranica c i d koje nisu paralelne. Ako je c=d trapez je jednakokraki. Srednja linija trapeza obeležava se sa m
Deltoid
Deltoid je četvorougao kod koga se dijagonale seku pod pravim uglom pri čemu jedna dijagonala polovi drugu.