Sličnost

 Definicja

Neka je k pozitivan realan broj, sličnost ravni π sa koeficijentom k je funkcija P_k:π→π takva da za svake dve tačke A i B ravni π, ako je P_k(A)=A₁ i P_k(B)=B₁, onda je  |A₁B₁|=k|AB|.

 

Svaka izomertija neke ravni je sličnost te ravni sa koeficijentom k.

Svaka homotetija H_o,k neke ravni je sličnost te ravni sa koeficijentom |k|.

 

Opšta definicija sličnosti

Dve figure Φ i Ψ su slične , u oznaci  Φ ~Ψ, ako postoji sličnost P koja preslikava  Φ na Ψ, tj. Ako je P( Φ)=Ψ

 

Za utvrđivanje sličnosti trouglova koristimo četiri stava:

I stav

Dva trougla ABC i A₁B₁C₁ su slična ako i samo ako su dve  stranica jednog trougla proporcionalne odgovarajućim stranicama drugog trougla, a uglovi zahvaćeni ovim stranicama jednaki su među sobom.

II stav

Trouglovi ABC i A₁B₁C₁ su slični ako i samo ako su dva ugla jednog trougla jednaka sa dva odgovarajuća ugla drugog.

III stav

Trouglovi ABC i A₁B₁ C₁ su slični ako i samo ako su im sve odgovarajuće stranice proporcionalne.

IV stav

Dva trougla ABC i A₁B₁ C₁ su slična ako i samo ako su dve stranice jednog trougla proporcionalne odgovarajućim stranicama drugog , uglovi naspram dveju od tih odgovarajućih stranica podudarni , a naspram drugih dveju odgovarajućih stranica su oba ugla oštra , oba prava ili oba tupa.

Iz navedenih stavova možemo zaključiti da je :

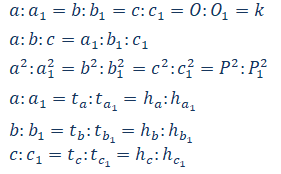
a,b,c,a₁,b₁,c₁– stranice sličnih trouglova O obim P-površina, t težišna duž, h visina trougla,k je koeficijent sličnosti.

 

 

Povratak na stranu Planimetrija