Neka je u ravni π data kružnica L( direktrida, vodilja ) i tačka S (V), tačka koja ne pripada ravni π . Skup tačaka svih pravih u prostoru koje sadrže tačku S i jednu tačku kružnice L , obrazuju površ koju nazivamo kružna konusna površ.
Tačka S je vrh konusne površi.
Kupa je telo ograničeno konusnom površi između temena S i ravni α i krugom koji pripada ravni α .
Ako je prava koja sadrži tačku S i centar kruga osnove, normalna na ravan osnove kupe, tada je kupa prava. Ako ovaj uslov nije ispunjen tada je kupa kosa.
Aminacija : Konusna površ i kupa
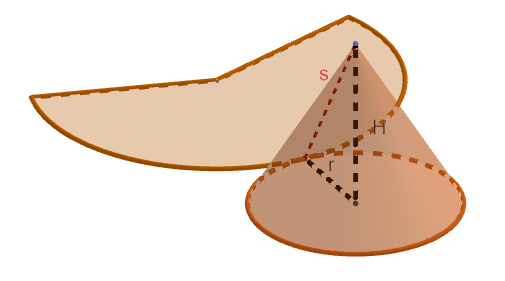
Deo konusne površi kod kupe nazivamo omotačem kupe, a krug kojim je ograničena – osnovom ili bazom. Ako je centar osnove kupe normalna projekcija vrha kupe na ravan osnove, tada takvu kupu zovemo prava kupa, u suprotnom je to kosa kupa.
Prava kupa je ograničena delom konusne površi (omotač) i jednim krugom, osnova. Ako je krug poluprečnika r, njegova površina je B=r2π. Ako omotač razvijemo u ravan dobićemo jedan kružni isečak čiji je poluprečnik jednak dužini izvodnica, koju označavamo sa s a dužina kružnog luka jednaka obimu kruga osnove, odnosno 2rπ.
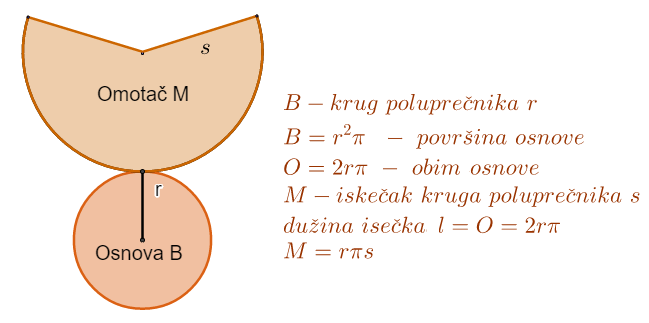
Površina omotača jednaka M= rπs. Dakle površina prave kupe, čiji je poluprečnik r, a dužina izvodnice s, jednaka je
P=B+M=r2π+rπs=rπ(r+s),
a njena zapremina V=r2πH.
Ravni preseci kupe i ravni
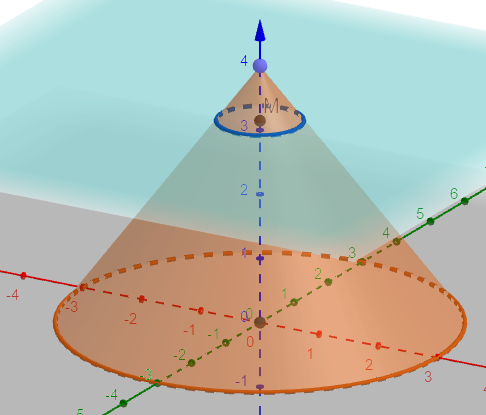
Presek kupe i ravni koja je paralelna osnovi kupe
Presek kupe i ravni paralelene osnovi , jeste krug homotetičan osnovi kupe.
Animacija: Kupa i ravan -paralelan presek
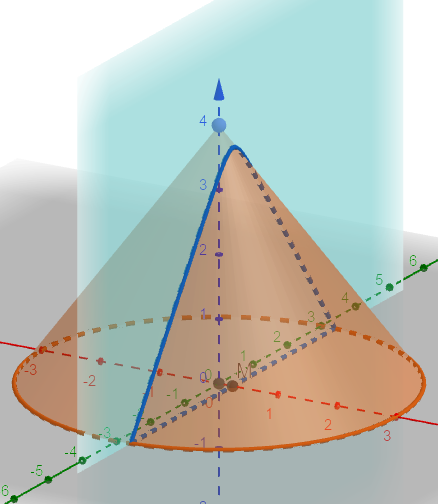
Presek kupe i ravni koja je normalna na ravan osnove kupe
Presek kupe i ravi koja je noramalna na osnovu kupe je tačka, zatvorena parabola, trougao… Ako ravan sadrži osu kupe- osni presek kupe.
Animacija: Kupa i ravan -Normalan presek
Presek kupe i ravni koja nije ni paralelna ni normalna na ravan osnove kupe
Presek ravni koja nije paralelna ravni i ne zaklapa ugao od π/2 sa ravni osnove, naziva se kos presek. Presek može biti, tačka, elipsa, zatvorena parabola…
Animacija: Kupa i ravan -kos presek
Zarubljena kupa
Ako kupu presečemo jednom ravni koja je paralelna sa ravni osnove, dobićemo dva tela: jedanu (manju) kupu i telo koje ćemo nazvati zarubljena kupa. Zarubljena kupa je, dakle, ograničena sa delom konusne površi (omotačem) i sa dva kruga koji pripadaju paralelnim ravnima.
Koristeći se formulom za izračunavanje površine prave kupe, izračunaćemo površinu prave zarubljene kupe. Neka su dati poluprečnici r i r1 osnova zarubljene kupe i dužina izvodnice s. Dopunimo zarubljenu kupe do prave kupe, i njenu izvosnicu označimo sa s1.
Površina osnova prave zarubljene kupe se lako izračunavaju: B=π r2, B=π r12.
Površinu omotača nalazimo kao razliku površina veće i manje kupe. Pa je površina omotača jednaka
M=π rs1−π r1(s1−s)=π(r−r1)s1+π r1s,
još je potrebno izraziti s1 u funkciji od r,r1 i s. Iz sličnosti pravouglih trouglova, čije su hipotenuze s i s1, imamo odnos (r−r1):r=s:s1, odakle je![]() . Sada dobijamo
. Sada dobijamo
M=πrs+πr1s=π(r+r1)s.
Dakle, površina prave zarubljene kupe je:
P=B1+B+M=r2π+r12π+π(r+r1)s.
