Neka je dat jedan n-tostrani rogalj Vp1,p2,p3,…,pn i jedna ravan α koja seče sve ivice roglja a ne sadrži njihov vrh. Skup svih tačaka datog roglja koje su sa iste strane ravni α sa koje je i vrh roglja, i u ravni α, naziva se n-tostrana piramida.
Visina bočne strane piramide koja polazi iz vrha piramide naziva se apotema i odgovara toj bočnoj strani. Ako je piramida pravilna to je apotema te piramide (sve apoteme su jednake)
Piramida je pravilna ako joj je osnova pravilan mnogougao i ako normala, postavljena kroz njen vrh na ravan osnove, prodire tu ravan kroz presek osa simetrija osnove. Ako je, međutim, ispunjen samo drugi uslov a osnova piramide nije pravilan mnogougao, tada kažemo da je piramida prava.
Površina piramide se nalazi slično kao i površina prizme. Ako obeležimo površinu piramide sa P, površinu osnove sa B, a površinu omotača sa M, imaćemo P=B+M. Pod površinom omotača, kao i kod prizme, podrazumevamo zbir površina bočnih strana. Zapremina piramide je V=BH/3
Ravni preseci piramide i ravni
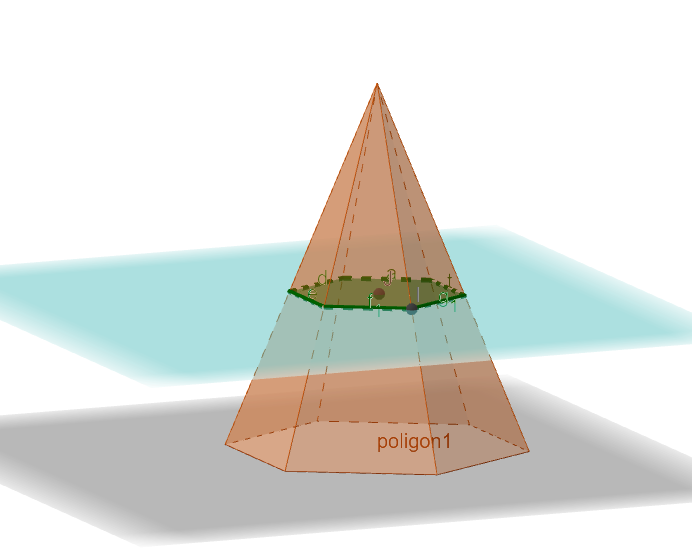
Presek piramide i ravni paralelene osnovi
Presek piramide i ravni koja je paralelna bazi n-tostrane piramide je n-tostrani mnogougao koji je homotetičan n-tostranom mnogouglu u osnovi.
Animacija: Paralelan presek
Presek piramide i ravni normalne na osnovu
Ravan koja je normalna na ravan osnove piramide sa piramidom gradi normalan presek koji može biti tačka, duž , trougao, četvorougao…
Animacija: Normalan presek na osnovu
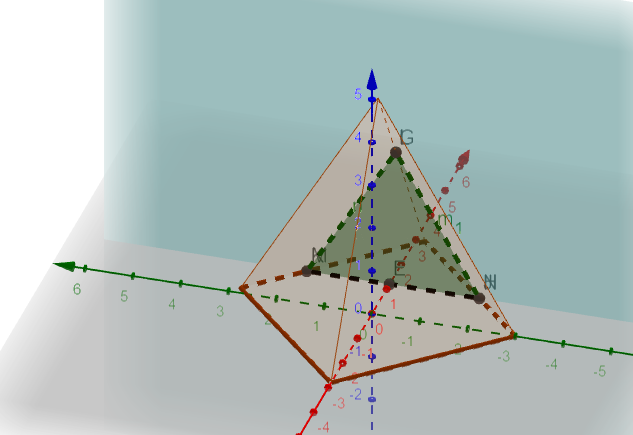
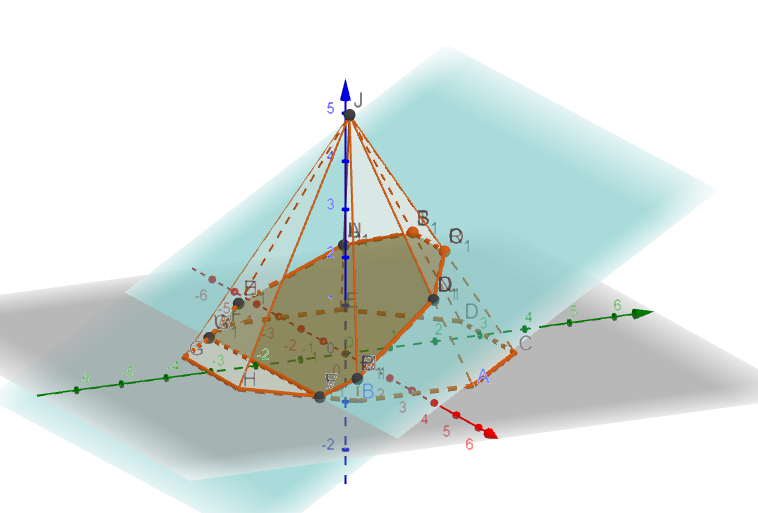
Presek piramide i ravni koja nije ni paralelena ni normalna na ravan osnove
Ravan koja nije normalna ni paralelna ravni osnove piramide sa piramidom ima kos presek.
Animacija : Kos presek
Zarubljena piramida
Sem prizme i piramide, u stereometriji često srećemo i zarubljenu piramidu koja se dobija kada se piramida preseče nekom ravni paralelnom osnovi.
Neka je data piramida VA1,A2,A3,…,An i neka je mnogougao B1,B2,B3,…,Bn jedan njen paralelni presek. Skup svih tačaka date piramide koje su između ravni mnogouglova A1,A2,A3,…,An i B1,B2,B3,…,Bn i tačaka koje pripadaju ovim mnogouglovima naziva se zarubljena piramida.
Površina zarubljene piramide se sastoji od dve osnove, koje su međusobno slični mnogouglovi i omotača. Kao i ranije pod površinom omotača ćemo podrazumevati zbir površina bočnih strana. Ako površinu zarubljene piramide označimo sa P, površine njenih osnova sa B1 i B2, a površinu omotača sa M, tada je P=B1+B2+M. Zapremina zarubjene pramide je ![]()
