Autor: D.Bajović www.promath.in.rs
Permutacije bez ponavljanja
Kako prepoznati permutacije bez ponavljanja?
Osnovni problem kombinatorike je određivanje broja načina na koji se neki elementi skupa A={a1, a2, a3, a4, …, an-1, an},n∈N, mogu rasporediti po nekom datom pravilu.
Potrebno je odrediti dve karakteristike rasporeda.
Prva karakteristika je da li je bitan redosled izbora ili ređanja elemenata skupa. Ako je redosled bitan i bira se k elemenata, onda se dobijaju uređene k-torke ili nizovi od k elemenata. Ako redosled nije bitan onda se dobijaju neuređene k-torke.
Druga karakteristika je da li se elementi mogu ponavljati ili ne.
Na osnovu tih karakteristika razlikuju se tri osnovna tipa rasporeda.
1. Permutacije;
2. Varijacije i
3. Kombinacije
Neka je dat skup , A={a1, a2, a3, a4,…, an-1, an},n∈N,. Pod permutacijom od n elemenata bez ponavljanja skupa A podrazumeva se svaka uređena n-torka ili niz od n elemenata skupa A, pri čemu se svaki elemenat pojavljuje tačno jedanput.
Kod permutacija je bitan redosled izbora elemenata, tj. redosled ređanja elemenata u niz. Raspoređuju se svi elementi skupa A. Permutacije ovog tipa biće obeležavane sa P, a ukupan broj permutacija od n elemenata bez ponavljanja će se obeležavati sa P(n).
Primer 1.
Koliko se različitih reči može formirati od slova reči „KOMBINAT“ (dobijene reči ne moraju imati smisla).
Pri fomiranju reči bitan je redosled izbora slova, učestvuju sva slova i nema ponavljanja slova, a to znači da su reči permutacije bez ponavljanja od 8 elemenata. Broj ovakvih reči može da se odredi kao što su rešavani prethodni primeri.
Formiraju se osmočlani izbori.
Prvo slovo biramo na osam načina, drugo na sedam i redom
Ukupan broj reči je
8 7 6 5 4 3 2 1
P(8)=8·7·6·5·4·3·2·1)=8!
■
Ako skup ima n elemenata onda se sličnom logikom može doći do formule za određivanje ukupnog broja permutacija bez ponavljanja od n elemenata.
P(n)=n·(n-1)·(n-2)…3·2·1=n! gde n! se čita n faktorijel.
Primer 2.
Koliko se različitih osmocifrenih brojeva može dobiti od skupa A = {0, 1, 2, 3, 4, 5, 6, 7}, ako se svaka cifra pojavljuje tačno jedanput.
Ti brojevi su permutacije bez ponavljanja, ali se od ukupnog broja permutacija moraju odbaciti permutacije kod kojih je nula na prvom mestu.
X=P(8)-P(7)=8!-7!=8·7!-7!=7·7!
Zadatak se mogao rešiti i starom logikom bez formula. Prvu cifru biramo na sedam načina jer su na raspolaganju cifre bez nule. Na drugom mestu može da se bira nula, ali je jedna cifra već odabrana pa preostaje sedam cifara. Treću cifru biramo na 6 načina, četvrtu na 5, itd.
7 7 6 5 4 3 2 1
Permutacije sa ponavljanjem
Neka je dat skup A={a1, a2, a3, a4, …, am-1, am},m∈N, . Pod permutacijom od n elemenata sa ponavljanjem podrazumeva se svaka uređena n-torka elemenata skupa A, pri čemu se elemenat a1 ponavlja k1 puta, elemenat a2 ponavlja k2 puta, … elemenat am ponavlja km puta, i k1+k2+…+km=n.
Ukupan broj permutacija sa ponavljanjem se računa po formuli
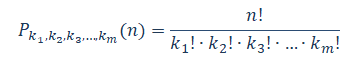
Primer 1.
Koliko se različitih reči može formirati od slova reči „MATEMATIKA“
Slovo M se ponavlja 2 puta, slovo A 3 puta, T – 2 puta, E – jedanput, I – jedanput i K jedanput.
n=2+3+2+1+1+1=10
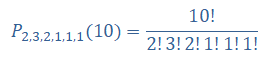
Primer 2.
Koja je po redu permutacija AVALA od početne permutacije AAAVL?
Napomena: pri formiranju permutacija poštuje se leksikografski poredak, u ovom primeru azbučni.
Primer 3.
Odrediti 500. permutaciju skupa {a, b, c, d, e, f}.
U ovom primeru se poštuje abc-dni poredak.
Permutacije – primer formiranja
Neka je dat skup cifara {1, 2, 3, 4}.
Cifre se ređaju u rastućem poretku pa je prva permutacija 1234.
Od ovog skupa se može formirati P(4)=4!=24 permutacije bez ponavljanja.
Redosled permutacija je
- 1234
- 1243
- 1324
- 1342
- 1423
- 1432
Jedinica ne može više biti na prvom mestu pa je sedma permutacija
- 2134
- 2143
- 2314
. . .
- 2431
- 3124
. . .
Poslednja permutacija je
- 4321
Svaki od elemenata skupa se pojavljuje na prvom mestu P(n):n = n!:n = (n-1)! puta.
Primer 4.
Koliko se različitih desetocifrenih brojeva može formirati od skupa {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} ako se svaka cifra pojavljuje tačno jedanput i jedinica ne može biti na prvom mestu, dvojka ne može biti na prva dva mesta i trojka ne može biti na prva tri mesta.
Za određivanje ukupnog broja ovakvih brojeva ne postoji formula koja bi se direktno primenila.
Ako je nula na prvom mestu broj neće biti desetocifren. Sa datim uslovima na prvoj poziciji mogu se koristiti cifre
I: {4, 5, 6, 7, 8, 9}
na drugoj poziciji ne mogu biti dvojka i trojka ali mogu nula i jedinica
II: {0, 1, 4, 5, 6, 7, 8, 9}
na trećoj poziciji ne može biti samo trojka
III: {0, 1, 2, 4, 5, 6, 7, 8, 9}
na ostalim pozicijama može biti bilo koja cifra
IV-X: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
Prvu cifru biramo na 6 načina. Za drugu poziciju se može birati jedna od 8 cifara, ali je jedna već izvučena pa se druga cifra bira na 7 načina. Treća cifra se bira na 7 načina (od 9 cifara 2 su izvučene). Četvrta cifra se bira na 7 načina (izvučene su 3 cifra), peta na 6 načina (izvučene 4 cifre) itd.
Ukupan broj brojeva je
x = 6·7·7·7!
Napomena: Ako se prave permutacije bez ponavljanja skupa {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, onda nula može biti na prvoj poziciji.
