Autor: D.Bajović www.promath.in.rs
Varijacije bez ponavljanja
Kako prepoznati varijacije sa i bez ponavljanja?
Neka je dat skup A={a1,a2,a3,a4,…,an-1,an},n∈N. Pod varijacijom bez ponavljanja od n elemenata k-te klase skupa A podrazumeva se svaka uređena k-torka različitih elemenata skupa A, pri čemu je k <= n.
Kod varijacija je bitan redosled izbora elemenata, tj. redosled ređanja elemenata u niz. Ako je k = n, onda su varijacije bez ponavljanja isto što i permutacije bez ponavljanja.
Primer 1.
Koliko se različitih petocifrenih brojeva može formirati od skupa {1, 2, 3, 4, 5, 6, 7, 8, 9} tako da se svaka cifra pojavljuje najviše jedanput.
Prvu cifru biramo na 9 načina, drugu na 8, treću na 7, četvrtu na 6 i petu na 5 načina.
Ovakvih brojeva ima x = 9·8·7·6·5 = 15120
Ukupan broj varijacija od n elemenata k-te klase bez ponavljanja jednak je
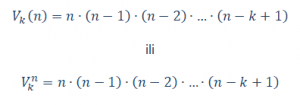
U proizvodu su uzastopni prirodni brojevi i ima ih k.
Označavanje ovog broja nije jednoznačno.
Primer 2.
Koliko se različitih petocifrenih brojeva može formirati od skupa {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} tako da se svaka cifra pojavljuje najviše jedanput.
x= V5(10)- V4(9)
x=10·9·8·7·6-9·8·7·6=9·9·8·7·6
Zadatak se može rešiti tako što odredimo ukupan broj varijacija i odbacimo varijacije kod kojih je nula na prvom mestu.
Zadatak se mogao rešiti i bez formula. Posmatramo svaku poziciju i određujemo na koliko načina biramo cifre.
Prvu cifru biramo na 9 načina (bez nule), drugu na 9 (nula može da se bira ali je jedna cifra već izvučena), treću na 8, četvrtu na 7 i petu na 6 načina.
Ovakvih brojeva ima x = 9·9·8·7·6
Primer 3.
Koliko se različitih petocifrenih brojeva deljivih sa 4 može formirati od skupa {0, 1, 2, 3, 4, 5, 7, 9} tako da se svaka cifra pojavljuje najviše jedanput?
Primer 4.
Dokazati da je Vn-1(n)=Vn(n)=n!
Primer 5.
Rešiti jednačine
a) V2(x)=380
b) V4(x): V5(x-1)=1:3
c) V3(2x+4): V4(x+4)=2:3
Varijacije sa ponavljanjem
Neka je dat skup A={a1,a2,a3,a4,…,an-1,an},n∈N. Pod varijacijom sa ponavljanjem od n elemenata k-te klase skupa A podrazumeva se svaka uređena k-torka elemenata skupa A.
Svaki elemenat skupa A se može ponoviti najviše k puta, pri čemu k može biti manje, jednako ili veće od n.
Kod permutacija sa ponavljanjem broj pojavljivanja svakog elementa je fiksiran a kod varijacija sa ponavljanjem određen je najveći broj ponavljanja svakog elemeta (elemenat se ne mora pojaviti).
Primer 1.
Koliko se različitih dvocifrenih brojeva može formirati od skupa {1, 2, 3}?
To su brojevi {11, 12, 13, 21, 31, 22, 23, 32, 33}.
Svaka cifra se pojavila najviše dva puta.
U ovom primeru su nabrojani svi izbori.
Primer 2.
Koliko se različitih petocifrenih brojeva može formirati od skupa {1, 2, 3, 4, 5, 6, 7, 8, 9}?
U ovom primeru broj elemenata skupa je veliki pa bi nabrajanje bilo nepraktično.
Posmatramo pozicije izbora i na koliko načina se mogu odabrati.
Prvu cifru biramo na 9 načina (na raspolaganju je devet cifara), drugu cifru biramo opet na devet načina (cifre se mogu ponavljati pa su na raspolaganju sve cifre), treću, četvrtu i petu biramo na devet načina pa je ukupan broj brojeva
![]() k(n)=nk
k(n)=nk
Ukupan broj varijacija sa ponavljanjem od n elemenata k-te klase jedanak je
Primer 3.
Koliko se različitih petocifrenih brojeva može formirati od skupa {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}?
Zadatak se može rešiti tako što se odredi ukupan broj varijacija i odbace varijacije kod kojih je nula na prvoj poziciji.
_ _
x=![]() 5(10)-
5(10)- ![]() 4(10)=105-104=10·104-104=9·104
4(10)=105-104=10·104-104=9·104
II način
Posmatramo pozicije izbora i na koliko načina se mogu odabrati.
Prvu cifru biramo na 9 načina (cifare bez nule). Na ostalim pozicijama se cifre mogu birati na 10 načina (sve cifre).
9 10 10 10 10
x=9·10·10·10·10
Primer 4.
Koliko se Morzeovih znakova može formirati od elementarnih znakova . i –, ako se jedan znak sastoji od najviše pet elemetarnih znakova.
x=21+22+23+24+25=62
