Skupovi se najčešće obeležavaju velikim latiničnim slovima A,B ,…..X, Y,… , a elementi skupa malim latiničnim slovima a,b,…,x,y,…
Ako je x element skupa X , pišemo x ∈ X, a ako ne pripada skupu X, pišemo x ∉ X. Oznake ćemo čitati: “x pripada skupu X” ili “x je element skupa X”. Oznaku x∉X ćemo čitati “ x ne pripada skupu X” ili “ x nije element skupa X”
Članove skupa koji zadovoljavaju neko svojstvo (definiciju) S možemo zapisati
{x Ι S(x)} ili {x Ι x ima svojstvo S},
Ako imamo skup X={-1,0,1,2} i neka ja svojsto formiranja skupa A: x∈X i x∈N
A={xΙ x ∈X∧x ∈N }={1,2}
Skup maže biti prazan ako nema elemenata koji zadovoljavaju svojstvo po kom formiramo skup i obeležava se sa ∅.
Skupovi A i B su jednaki ako su svi elementi jednog skupa ujedno elementi drugog skupa, i obrnuto, svi elementi drugog skupa su elementi prvog skupa . Zapisujemo: A = B ako i samo ako (∀x) (x∈ A ⇔ x ∈ B )
Definicija:
Kažemo da je skup B podskup skupa A, što označavamo B⊂A, ako su svi elementi skupa B takođe i elementi skupa A, tj. B⊂ A ako i samo ako (∀x) (x ∈B ⇒x∈ A )
Relacija uvedena ovom definicijom se zove relacija inkluzije.
Prazan skup je podskup svakog skupa.
skupovne operacija
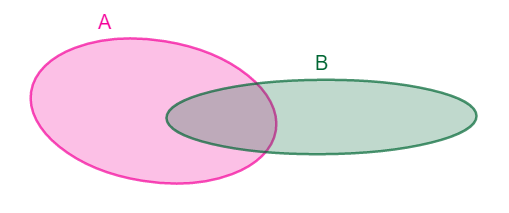
Neka su A i B skupovi na kojima će se definisati osnovne skupovne operacije.
Unija
Definicija:
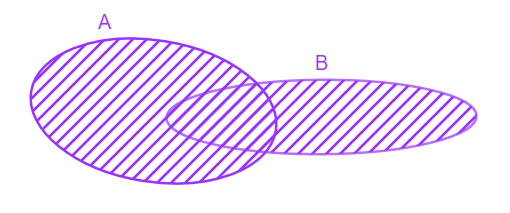
Skup svih elemenata koji su elementi bar jednog od skupova A ili B , zove se unija skupova A i B i označava se sa A ∪ B.
A ∪ B={xΙx∈A ∨ x∈B}
Na dijagramu bi to izgledalo ovako:
Presek
Definicija:
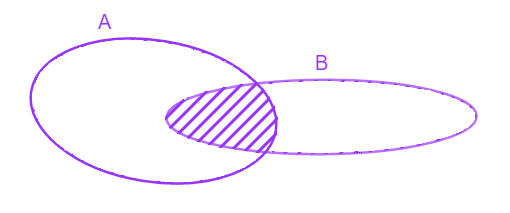
Skup svih elemenata koji su elementi skupa A i skupa B zove se presek skupova A i B i obeležava se sa A ∩ B.
A ∩ B={xΙx∈A ∧ x∈B}
Razlika
Definicija:
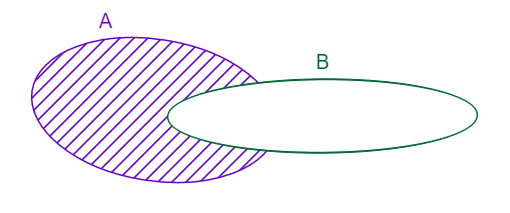
Skup svih elemenata koji su elementi skupa A ali nisu elementi skupa B, zove se razlika redom skupova A i B u oznaci A
B.
AB={ xΙ x∈A ∧ x∉B }
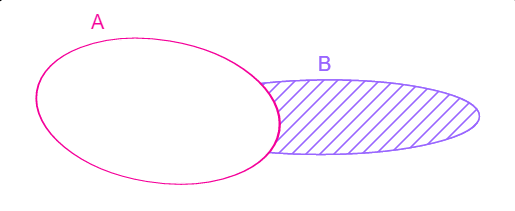
Razlika
Definicija:
Skup svih elemenata koji su elementi skupa B ali nisu elementi skupa A zove se razlika redom skupova B i A u oznaci BA.
BA={ xΙ x∈B ∧ x∉A }
Simetrična razlika
Definicija:
Skup (AB)∪(BA) naziva se simetrična razlika i najčešće se obeležava sa Δ
AΔB= (AB)∪(BA). AΔ B={xΙ x∈A ∧ x∉B }∪ {xΙ x∈B ∧x∉A }
Na dijagramu je:
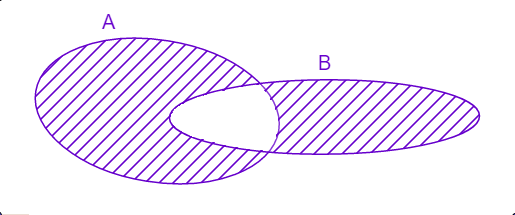
Partitivni skup
Definicija:
Skup svih podskupova skupa A naziva se partitivni skup skupa A i obeležava se sa P(A).
Komplement skupa
Definicija:
Skup svih elemenata koji nisu sadržani u posmatranom skupu.
Komplement najčešće obeležavamo sa Ac
Ac={xΙ x∉ A}
Unija , presek i razlika su binarne skupovne operacije, dok je komplement skupa unarna operacija.
Dekartov proizvod
Dekartov proizvod skupova A i B je skup je skup uređenih parova (x,y), takvih da x∈A i y∈B:
AxB={(x,y)Ιx∈A ∧ y∈B}
Treba voditi računa da A×B≠B×A.
Zadaci:
Zadatak 2
Odrediti elemente skupova A, B, C, ako je AU B U C = {1,2,3,4,5, 6 } , (A ∩ C)U (B∩ C) = ∅ , AB ={1,3,5} , C B = (2,4) i (A∩B)C ={6 }.
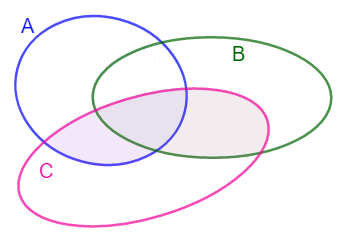
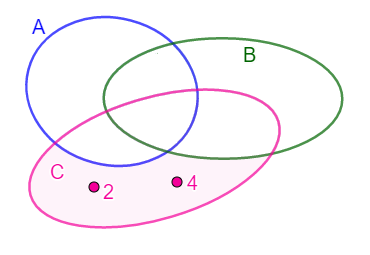
AU B U C = {1,2,3,4,5, 6 } Unija svih skupova nam daje informaciju koji elementi mogu biti u skupovima A,B, ili C.
(A ∩ C)U (B∩ C) = ∅ -prazan skup , osenčeno na slici nema elemenata.
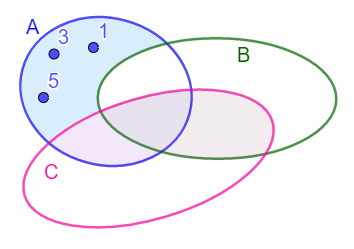
AB ={1,3,5} – na slici je osenčen plavo deo razlike skupova A i B u kom mogu biti brojevi poštujući prethodni uslov
C B = (2,4) i (A ∩ C)U (B∩ C) = ∅ osenčeni deo slike zadovoljava ova dva uslova i u tam delu su elementi 2 i 4.
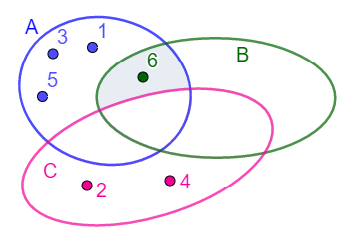
(A∩B)C ={6 }.
Rešenje zadatka
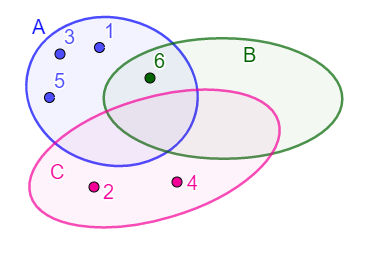
A={1,2,5,6},
B={6},
C={2,4}.
Zadatak 3
Dati sa skupovi A, B i C. Dokaži da važi:A(BUC)= (AB)∩(AC).
Dokaz:
Da bi dokazali tvrđenje zadatka neophodno je da znamo definicije skupovnih operacija i neke zakone zaključivanja:
A(BUC)= (AB)∩(AC).
x∈A(BUC)⇔x∈A∧x∉(BUC)⇔ po definiciji razlike dva skupa
⇔x∈A∧¬x∈(BUC)⇔ x∉ menjamo sa ¬x∈
⇔x∈A∧¬(x∈B ∨ x∈C)⇔ po definiciji unije dva skupa
⇔x∈A∧(x∉B ∧ x∉C)⇔ DeMorganov zakon ￢(p ∨ q) ⇔ ￢p ∧ ￢q
⇔(x∈A∧x∉B) ∧ x∉C⇔ zakon asocijacije p ∧ (q ∧ r ) ⇔ (p ∧ q) ∧ r
⇔(x∈A∧x∉B) ∧ x∉C∧x∈A⇔ x∈A i x∈A ∧ x∈A su ekvivalentni iskazi
⇔(x∈A∧x∉B) ∧(x∈A∧ x∉C)⇔
⇔(x∈AB) ∧(x∈AC)⇔ po definiciji razlike dva skupa
⇔(x∈(AB) ∩(AC)⇔ po definiciji preseka dva skupa
Zadatak 4
Dati su skupovi A, B, i C. Dokaži tvrđenje (AUB)∩C=(A∩C)U(B∩C).
x∈ (AUB)∩C⇔x∈ (AUB)∧x∈C⇔
⇔(x∈ A∨x∈B)∧x∈C⇔ po zakonu distribucije p ∧ (q ∨ r ) ⇔ (p ∧ q) ∨ (p ∧ r ),
⇔(x∈ A∧x∈C)∨(x∈B∧x∈C)⇔
⇔(x∈ A∩C)∨(x∈B∩C)⇔
⇔x∈(A∩C)U(B∩C)