Kao osnovne trigonometrijske funkcije navodimo y=sinx, y=cosx, y=tgx, y=ctgx.
Sve osnovne trigonometrijske funkcije su periodične , ali ime se osnovni period razlikuje i to sinx i cosx su sa osnovnim periodom 2π, a tgx i ctgx sa osnovnim periodom π.
Prema definisanosti osnovne trigonometrijske funkcije možemo podeliti na dve grupe :
- sinx i cosx su definicani D_f: x∈ (-∝,∝) i neprekidne su
- tgx D_f: ∀x∈R π/2+kπ, i ctgx D_f: ∀x∈R 0+kπ ikažemo da su ove funkcije prekidne.
Osnovne trigonometriske funkcije -y=sinx
Grafik funkcije je skup tačaka T čije su koordninate apscisa-vrednost ugla α i ordinata- AC= A1C1 ,T(α,A1C1).
Koordinate bilo koje takčke na grafiku funkcije su uređeni par nezavisno promenljive- apscisa i vrednosti funkcije za tu nezavisno promenljivu. U slučaju sinusne funkcije koordinate su vrednsot ugla α i sin(α) ,T(α , sin(α)). Vrednosti ugla α prikazujemo na x-osi od 0 za α=0 do α= 6.28=2π ili α=360o.
Vrednost funkcije sin(α) čitamo na y-osi AC= sin(α). Promene vrednosti ugla prati tačka A1 na x-osi a promene sin(α) tačka C1.

Konstrukciju grafika počinjemo tačkom T(0,0) za α=0° ,sinα=0 ,…, T(π/6,1/2) za za α=30° ,sinα=1/2,…, T(π/3,1.73/2) za za α=60° ,sinα=1.73/2,…, T(π/2,1) za za α=90° ,sinα=1,…, T(π,0) za za α=180° ,sinα=0,…, T(3π/2,-1) za za α=270° ,sinα=-1,…, T(2π,0) za za α=360° ,sinα=0.
U ispitivanju toka funkcije
U ispitivanju toka funkcije važne su sledeće tačke
1. Oblast definisanosti (vrednosti promenljive za koje je funkcija ima konačne vrednosti) Specijalno ovu funkciju posmatramo na intervalu (0,2π) i vidimo da je na tok intervalu definisana sve vrednosti α ∈(0,2π)
2. Nule funkcije: (preseci grafika funkcije sa x-osom) y=0, za α=0, α=π
3. Znak funkcije: (grafik funkcije iznad x ose y>0 ili ispod x-ose y<0), y>0, za α iz intervala (0, π), y<0, za α iz intervala (π,2π)
4. Monotonost funkcije: funkcija monotono opada za α iz intervala (π/2,3π/2), funkcija monotono raste za α iz intervala (0,π/2)U(3π/2, 2π)
5. Ekstremne vrednosti: maksimalna vrednost funkcije je 1 za α=π/2, minimalna vrednost funkcije je -1 za α=3π/2
6. Ograničenost funkcije: funkcija je ograničena -1<f(x)<1

Animacija: Grafik funkcije y=sinx
Osnovne trigonometriske funkcije y=cosx
Grafik funkcije je skup tačaka T čije su koordninate apscisa-vrednost ugla α i ordinata- vrednost funkcije AC= A1C1 ,T(α,A1C1).
Koordinate bilo koje takčke na grafiku funkcije su uređeni par nezavisno promenljive- apscisa i vrednosti funkcije za tu nezavisno promenljivu. U slučaju kosinusne funkcije koordinate su vrednsot ugla α i cos(α) ,T(α , cos(α)). Vrednosti ugla α prikazujemo na x-osi od 0 za α=0° do α= 6.28=2π ili α=360°.

Promene vrednosti kosinusne funkcije
Vrednost funkcije cos(α) čitamo na x-osi AC=cos(α). Promene vrednosti ugla prati tačka A1 na x-osi a promene funkcije cos(α) tačka C1. Konstrukciju grafika počinjemo tačkom T(0,1) za α=0° ,cosα=1 ,…, T(π/6,1,73/2) za za α=30° ,cosα=1.73/2,…, T(π/3,1/2) za za α=60° ,cosα=1/2,…, T(π/2,0) za za α=90° ,cosα=0,…, T(π,-1) za za α=180° ,cosα=-1,…, T(3π/2,0) za za α=270° ,cosα=0,…, T(2π,1) za za α=360° ,sinα=1.
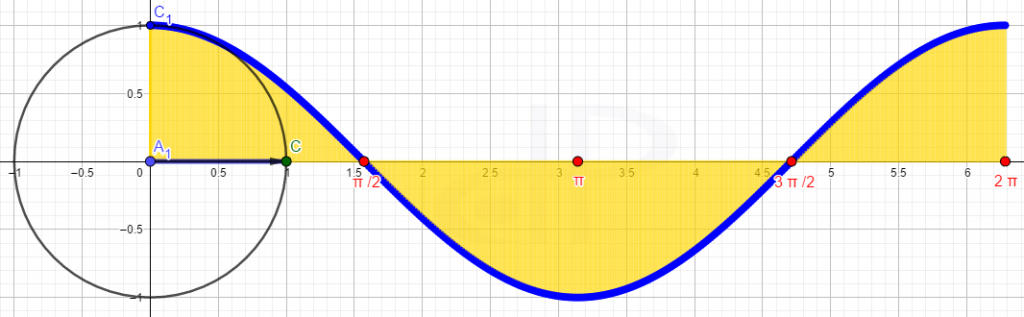
U ispitivanju toka funkcije važne su sledeće tačke
1. Oblast definisanosti (vrednosti promenljive za koje je funkcija ima konačne vrednosti) Specijalno ovu funkciju posmatramo na intervalu (0,2π) i vidimo da je na tok intervalu definisana za sve vrednosti α ∈(0,2π)
2. Nule funkcije: (preseci grafika funkcije sa x-osom) y=0, za α=π/2, α=3π/2
3. Znak funkcije: (grafik funkcije iznad x ose y>0 ili ispod x-ose y<0)
y>0, za α iz intervala (0, π/2)U (3π/2,2π)
y<0, za α iz intervala (π/2,3π/2)
4. Monotonost funkcije: funkcija monotono opada za α iz intervala (0, π) funkcija monotono raste za α iz intervala (π,2π)
5. Ekstremne vrednosti: maksimalna vrednost funkcije je 1 za α=0. Minimalna vrednost funkcije je -1 za α= π
6. Ograničenost funkcije: funkcija je ograničena -1<f(x)<1
Animacija : Grafik funkcije y= cosx
Osnovne trigonometriske funkcije y=tgx
Promene vrednosti tangensne funkcije
Vrednost funkcije tg(α) čitamo na pravoj x=1 i AC=tg(α). Promene vrednosti ugla prati tačka A1 na x-osi a promene funkcije ctg(α) tačka C1. Konstrukciju grafika počinjemo tačkom T(0,0) za α=0° ,tgα=0 ,…, T(π/6,1,73/3) za za α=30° ,tgα=1.73/3,…, T(π/4,1) za α=45° ,tgα=1 ,…,T(π/3,1.73) za α=60° ,tgα=1.73,…, T(π/2,∞) za α=90° ,tgα= ∞,…, T(3π/4,-1) za za α=135° , tgα=-1,…, T(π,0) za α=180° ,tgα=0,
Sa slike se vidi, da je osnovni period funkcije od 0 do π jer se posle π vrednosti funkcije y=tgα ponavljaju.
Funkcija uvek raste i na svom osnovnom periodu ima jednu nulu
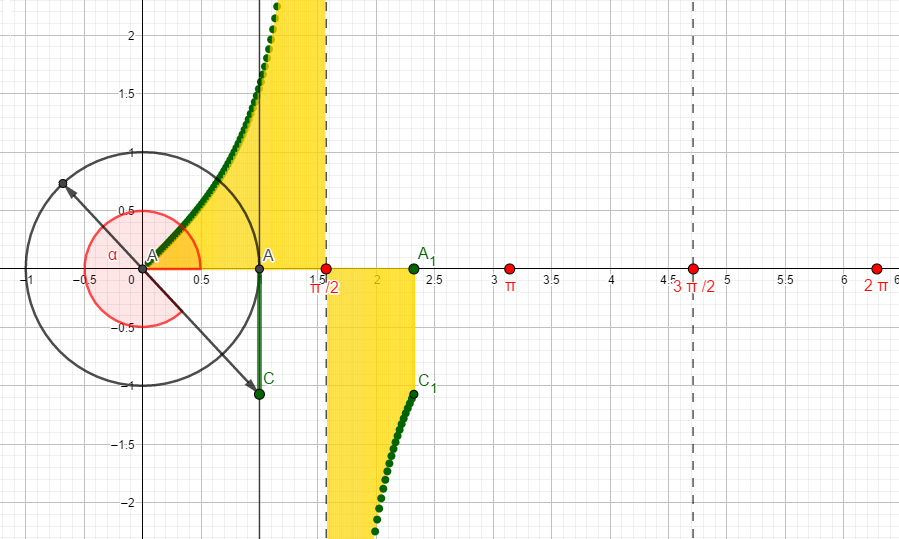
Ispitivanje toka funkcije y=tgx
- Oblast definisanosti (vrednosti promenljive za koje je funkcija ima konačne vrednosti) Specijalno ovu funkciju posmatramo na intervalu (π/2,3π/2) i vidimo da funkcija nije definisana nije definisana na njegovim krajevima.
- Nule funkcije: (preseci grafika funkcije sa x-osom) y=0, za α=0, α=π.
- Znak funkcije: (grafik funkcije iznad x ose y>0 ili ispod x-ose y<0).
y>0, za α iz intervala (0, π/2) U(π, 3π/2).
y<0, za α iz intervala (π/2,π) U(3π/2, 2π).
- Monotonost funkcije: funkcija monotono raste za α iz intervala (0,2π).
- Ekstremne vrednosti: nema jer funkcija ne menja monotonost.
- Ograničenost funkcije: funkcija nije ograničena.
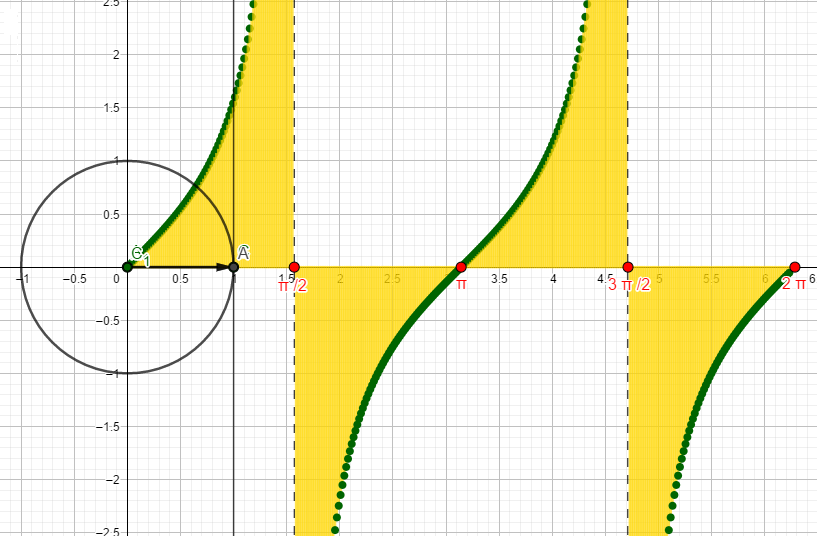
Animacija : Grafik funkcije y=tgx
Osnovne trigonometriske funkcije y=ctgx
Promene vrednosti kotangensne funkcije
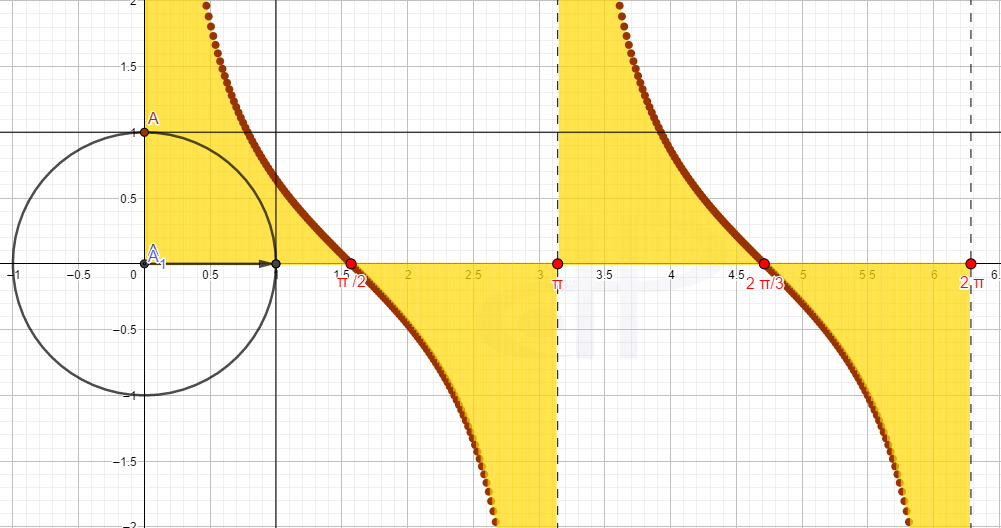
Vrednost funkcije ctg(α) čitamo na pravoj y=1 i AC=ctg(α). Promene vrednosti ugla prati tačka A1 na x-osi a promene funkcije ctg(α) tačka C1. Konstrukciju grafika počinjemo tačkom T(0,1) za α=0° ,ctgα=∞ ,…, T(π/6,1,73) za za α=30° ,ctgα=1.73,…, T(π/4,1) za α=45° ,ctgα=1 ,…,T(π/3,1.73/3) za α=60° ,ctgα=1.73/3,…, T(π/2,0) za α=90° ,ctgα= 0,…, T(3π/4,-1) za za α=135° , ctgα=-1,…, T(π,0) za α=180° ,ctgα=-∞,
Sa slike se vidi, da je osnovni period funkcije od 0 do π jer se posle π vrednosti funkcije y=ctgα ponavljaju.
Funkcija uvek opada i na svom osnovnom periodu ima jednu nulu.

- Oblast definisanosti (vrednosti promenljive za koje je funkcija ima konačne vrednosti) Specijalno ovu funkciju posmatramo na intervalu (0,π) i vidimo da funkcija nije definisana na njegovim krajevima.
- Nule funkcije: (preseci grafika funkcije sa x-osom) y=0, za α=0, α=π.
- Znak funkcije: (grafik funkcije iznad x ose y>0 ili ispod x-ose y<0).
y>0, za α iz intervala (0, π/2) U(π, 3π/2).
y<0, za α iz intervala (π/2,π) U(3π/2, 2π).
- Monotonost funkcije: funkcija monotono opada za α iz intervala (0,2π).
- Ekstremne vrednosti: nema jer funkcija ne menja monotonost.
- Ograničenost funkcije: funkcija nije ograničena.
Animacija: Grafik funkcije y=ctgx
