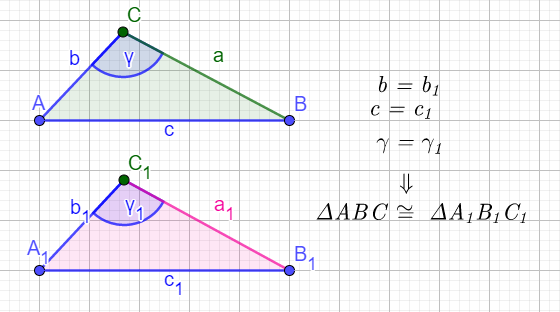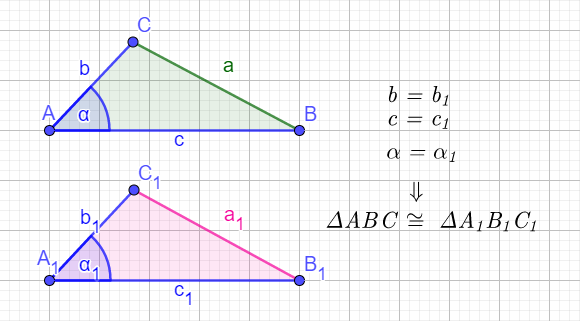
Podudarnost trouglova prvi stav- SUS
(stranica – ugao- stranica)
Ako dva trougla imaju jedake po dve odgovarajuće stranice i njima zahvaćen ugao (ugao između tih stranica), tada su ta dva trougla podudarna.
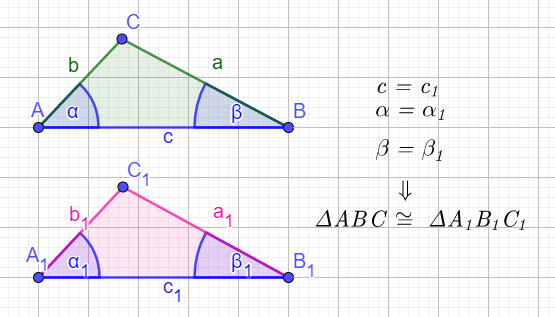
Podudarnost trouglova drugi stav –USU
(ugao – stranica – ugao)
Ako dva trougla imaju jednaku jednu stranicu i jednake na njoj nalegle uglove, tada su ti trouglovi podudarni.
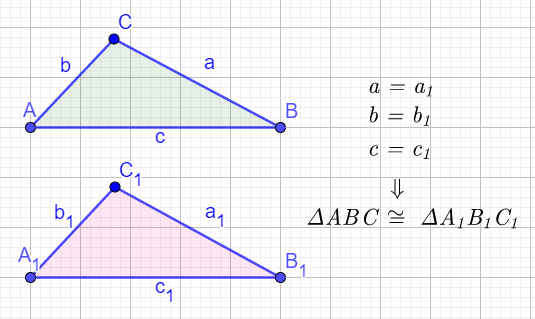
Podudarnosti trouglova treći stav – SSS
(stranica – stranica – stranica)
Ako su sve tri stranice jednog trougla jednake odgovarajućim stranicama drugog trougla, tada su ti trouglovi podudarni.
Podudarnost trouglova četvrti stav – SSU
(stranica – stranica – ugao)
Ako su dve stranice i ugao naspram duže od njih jednog trougla jednaki odgovarajućoj stranici i uglu drugog trougla, tada su ti trouglovi podudarni.