Šta je kružnica a šta krug? Kako glasi jednačina kružnice?
Kružna linija (kružnica) je skup tačaka u ravni sa osobinom da su sve jednako udaljene od jedne stalne tačke. Ta stalna tačka je centar kružnice, a konstantno rastojanje tačaka od centra je poluprečnik kružnice. Krug je skup tačaka u ravni sa osobinom da je rastojanje tih tačaka od jedne stalne tačke manje ili jednako od neke konstante (krug je unija kružne linije i tačaka iz unutrašnjosti). Jednačina kružnice predstavlja rastojanje između centra kružnice i tačke na kružnici.
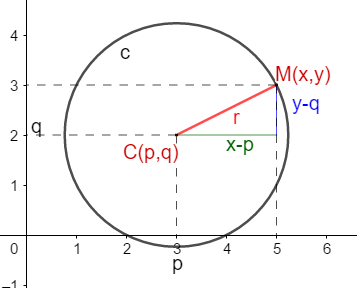
Rastojanje r, tačke M(x,y) od centra kruga C(p,q) računa se Na osnovu Pitagorine teoreme
(x-p)2+(y-q)2=r2
Ako je centar kruga u koordinatnom početku C(0,0) onda je njegova jednačina
x2+y2=r2
Jednačina kružnice
primer 1.
r2=(-1+4)2+(-1-3)2
pa je jednačina kruga (x+4)2+(y-3)2=25
Jednačina krive drugog reda u opštem obliku glasi Ax2+Bxy+Cy2+Dx+Ey+F=0, a jednačina kruga u opštem obliku Ax2+Ay2+Dx+Ey+F=0.
Koeficijenti uz kvadratne članove moraju biti jednaki i nema mešovitog člana Vhu. Jednačina se može podeliti sa A i dobija se jednostavniji oblik koji uz kvadratne članove ima koeficijente jednake 1.
x2+y2+(D/A)x+(E/A)y+(F/A)=0
(x+D/2)2+(y+E/2)2=(D2+E2-4F)/4
uz uslov D2+E2-4F>0
Koordinate centra kruga i poluprečnik se mogu odrediti pomoću formula
P=-D/2,, q=-F/2 r2=p2+q2-F
primer 2.
Odrediti centar i poluprečnik kruga koji je dat jednačinom
x2+y2-6x+4y-23=0
Datu jednačinu kruga dopunimo do kvadrata binoma po h i po
x2-6x+32+y2+4y+22-32-22-23=0
(x-3)2+(y+2)2=36
Iz jednačine se pročitaju koordinate centra S(3,-2) i poluprečnik r = 6.
Jednačina kružnice
primer 3 3.

A ∈k ⇒ (-2-p)2+(-6-q)2=r2
B ∈k ⇒ (7-p)2+(-3-q)2=r2
C ∈k ⇒ (2-p)2+(2-q)2=r2
————————————————
4+4p+p2+36+12q+q2=49-14p+p2+9+6q+q2
4+4p+p2+36+12q+q2=4-4p+p2+4-4q+q2
————————————————-
18p+q=18
8p+16q=-32
————————
C ∈k ⇒ (2-2)2+(2+3)2=25
Jednačina datog kruga je (x-2)2+(y+3)2=25
Решење се могло добити и тако што се одреде симетрале две тетиве круга и у пресеку тих симетрала налази се центар круга.
Једначине симетрала су
s1:2x-2y-10=0
s2:x+2y+4=0

Jednačina kružnice
primer 4.
A ∈k ⇒ (-6-p)2+(5-q)2=r2
B ∈k ⇒ (2-p)2+(1-q)2=r2
C(p,q) ∈l ⇒ 2p-3q=-9
————————————————
36+12p+p2+25-10q+q2=4-4p+p2+1-2q+q2
2p-3q=-9
———————————————————————-
r2=(2+3)2+(1-1)2=25
Jednačina datog kruga je (x+3)2+(y-1)2=25
Tangente kroz tačku koja pripada krugu
Kružnica i prava primer 1.
K: x2+y2+4x-4y-17=0
(x+2)2+(y-2)2=25
p=-2, q=2, r=5, x0=1, y0=-2
