Pojam prave je jedan od osnovnih pojmova elementarne geometrije. Polazimo od toga da je određena sa dve tačke odnosno postoji jedna i samo jedna prava koja sadrži dve date tačke. Jednačina prave ima implicitni, eksplicitni i segmenti oblik .
Uzmimo da su to tačke A(x1,y1) i B(x2,y2) u Dekartovom koordinatnom sistemu. A i B određuju pravu AB.
Neka je M proizvoljna tačka prave AB sa koordinatama M(x,y). Za ove tri tačke važi: površina trougla MAB je jednaka nuli.
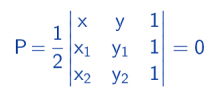
Rešavanjem determinante dobijamo

Jednačina prave – implicitni oblik
Rešavanjem jednačine i uvođenjeim smene dobili smo implicitni ili opšti oblik jednačine prave
Razmotrićemo specijalne slučajeve.
Ako tačke A i B imaju jednake apsisne koordinate ⇒ prava je paralelna y-osi. Jednačina prave koja je paralelna y-osi (apscisnoj osi) je: x = ݊a (a∈R)
Ako tačke A i B imaju jednake ordinatne koordinate ⇒ prava je paralelna x-osi.a) Jednačina prave koja je paralelna x-osi (apscisnoj osi) je: y= ݊n
Eksplicitni oblik jednačine prave
Ako iz jednačine
![]()
izrazimo y

i uvedemo smenu

dobićemo y=kx+n -eksplicitni oblik jednačine prave.
k je koeficijent pravca i predstavlja tangens ugla koji prava zaklapa sa x-osom k=tgφ.
n je odsečak na y-osi.
Segmentni oblik jednačine prave
Neka prava sa koordinatnim osama gradi odsečke ܱm na x-osi i n na y-osi
Jednačina x/m+y/n=1
se naziva segmentni oblik jednačine prave.
Jednačina prave kroz jednu i dve tačke
Iz istog izvora dobićemo još dve jednačine prave.

Dve prave koje su paralelne zaklapaju isti ugao sa x-osom . Ako su uglovi jednaki jednaki su k1=k2=tgφ.
Za dve prave koje zaklapaju ugao od 90 stepeni važi k1=-1/k2=tgφ.

