Funkcije definišemo kao preslikavanje elemenata jednag skupa na drugi.
Skup f je funkcija iz A u B, u oznaci f:A→ B, ako važe sledeći uslovi:
1. f⊆AxB
2. za svako x iz A postoji jedan element y iz B takav da skup (x,y)∈f.
Ako f: A→ B, skup A se naziva domen ili oblast definisanosti a skup B kodomen ili oblast vrednosti funkcije f.
Kompozicija funkcija f:A→ B i g: B→ C je funcija h: A→ C definisana sa h(x)=g(f(x)). Funkcija h se označava sa g o f. Dakle, (g ο f)(x)=g(f(x))
Funkcija f:A→ B je :
- 1-1 funcija (jedan na jedan), ako je za svako x1 ,x2 iz A tačna implikacija x1≠x2⇒ f(x1)≠ f(x2), f(x1)=f(x2)⇒x1=x2
- Na funkcija, ako za svako y iz B postoji x iz A tako da je f(x)=y
- Bijekcija ako je 1-1 funkcija i na funkcija
Ako je f:A→B bijektivna funkcija , tada je inverzna funkcija za f funkcija f-1:B→A takva da za svako x iz A važi f-1(f(x))=x i za svako y iz B važi da je f(f-1 (y))=y. Grafici inverznih funkcija simetrični su u odnosu na simetralu prvog i trećeg kvadranta ( y=x ).
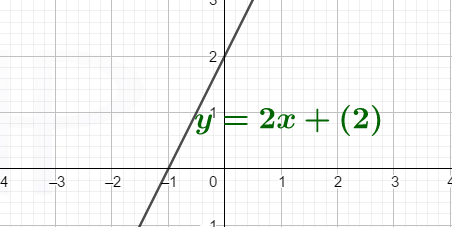
Ako su domen i kodomen funkcije, skupovi sa beskonačno mnogo elemenata, funkciju možemo grafićki predstaviti u pravouglom koordinatnom sistemu. Na slici je dat grafik funkcije y=2x+2.
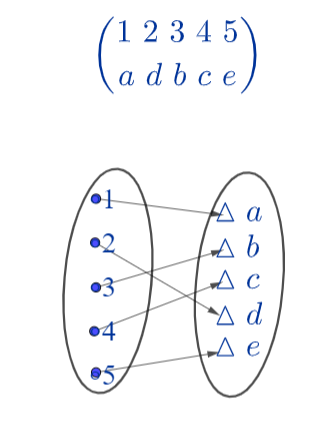
Ako su domen i kodomen funkcije ,skupovi sa konačno mnogo elemenata ,funkciju možemo grafićki prikazati tako što navedemo elemente domena i kodomena i i linijama povežemo odgovarajuće elemente.
Povratak na stranu matematička logika i skupovi
Na interaktivnoj strani inverzna funkcija može se naučiti postupak odreživanja inverzne funkcije ili proveriti znanje .
Na interaktivnoj strani kompozicija funkcija može se naučiti postupak odreživanja složene funkcije ili proveriti znanje .
