Relacije

Relacije predstavljaju veze (odnose) između izvesnih objekata. Najčešće se radi o vezi dva objekta, to su binarne relacije. U matematici se relacije definišu skupovnom terminologijom.

Definicija

Za ρ kažemo da je binarna relacija r na skupu A  ako je ρ ⊆ A².

Ako (a, b) ∈ ρ kažemo da je a u relaciji ρ sa b i pišemo a ρ b, ako (a, b) ∉ρ kažemo da a nije u relaciji ρ sa b i pišemo aρb.

Relacija ρ = ∅ je prazna relacija, a   r = A² je puna relacija.

Primer:

Na skupu A = {1, 2, 3} primeri binarnih relacija su

ρ₁ = {(1, 1), (2, 2), (3, 3)}, tj. ρ _1 = ” = ” (jednakost u skupu A)

ρ₂ = {(1, 2), (1, 3), (2, 3)}, tj. ρ _2 = ” < ”.

Svakoj binarnoj relaciji r skupa A odgovara funkcija f_r: A² → {1, 0}, data na sledeći način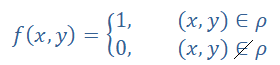koja se zove karakteristična funkcija relacije ρ.

Dakle, binarnu relaciju možemo zadati i njenom karakterističnom funkcijom. U slučaju konačnog skupa A, funkciju f_ρ obično zadajemo tablicom.

Neka je A = {a, b, c, d, e}. Binarnu relaciju ρ možemo zadati navođenjem elemenata, npr.

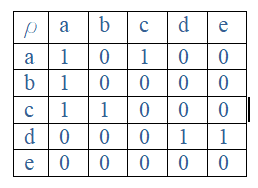
• r = {(a, a), (a, c), (b, a), (c, a), (c, b), (d, d), (d, e)}
• tablicom karakteristične funkcije

 

 

Primer

(1) Relacija ρ = {2, 4, 6, . . . } ⊆ N je unarna relacija skupa N. Ona izražava osobinu „biti paran broj“.

(2) ρ = {(x, y, z)|x +y = z} ⊆ N3 je ternarna relacija skupa N.

(3) Ako je A skup tačaka na pravoj, onda se svojstvom „x je između y i z“ definiše jedna ternarna relacija na A.

Primer

Primenom skupovnih operacija na relacije ρ₁ = {(1, 1), (2, 2), (3, 3)} i  ρ₂ = {(1, 2), (1, 3), (2, 3)} dobijamo

ρ₁ ∪ ρ₂ = {(1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3)} = ” ≤ ”,

ρ₁∩ ρ₂ = ∅,

A² ρ₁ = {(1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2)} = ” ≠ ”,

A²ρ₂= {(1, 1), (2, 1), (3, 1), (2, 2), (3, 2), (3, 3)} = ” ≥ ”.

= {2, 4, 6, . . . } ⊆ N je unarna relacija skupa N. Ona izražava

osobinu „biti paran broj“.

(2) ρ = {(x, y, z)|x +y = z} ⊆ N3 je terarna relacija skupa N.

(3) Ako je A skup tačaka na pravoj, onda se svojstvom „x je između y i z“

definiše jedna ternarna relacija na A.

 

Osnovne osobine koje binarna relacija može imati su: refleksivnost, simetričnost, antisimetričnost i tranzitivnost.

 

Definicija

Binarna relacija ρ skupa A je:

(R) refleksivna ako (∀ x ∈ A) x ρ x;

(S) simetrična ako (∀ x, y ∈ A) (x ρ y ⇒ y ρ x);

(A) antisimetrična ako (∀ x, y ∈ A) (x ρ y ∧ y ρ x ⇒ x = y);

(T) tranzitivna ako (∀ x, y, z ∈ A) (x ρ y ∧ y ρ z⇒x ρ z).

Jedina relacija skupa A koja ima sve četiri navedene osobine (RSAT) je relacija jednakosti.

Primer

(1) Na skupu A = {1, 2, 3}

• ρ₁ = {(1, 1), (1, 2), (1, 3)} je (A) i (T), a nije (R), niti (S);
• ρ ₂ = {(1, 2), (2, 1)} je (S), a nije (R), nije (A) i nije (T);
•  ρ ₃ = {(1, 1), (1, 2), (2, 1), (2, 2), (3, 3)} je (R), (S) i (T).

(2) Neka je na skupu S definisana relacija r na sledeći način:

x ρ y akko x poznaje y.

Ova relacija je (R) i (S), a nije (A), niti (T).

 

Relacije ekvivalencije

Definicija

Binarna relacija ρ  skupa A je relacija poretka ako je refleksivna, simetrična i tranzitivna (RAT).

Definicija

Binarna relacija ρ  skupa A je relacija ekvivalencije ako je refleksivna, simetrična i tranzitivna (RST).

Relacija ekvivalencije se obično označava sa ∼ (čita se tilda). Primeri relacija ekvivalencije: jednakost (na bilo kom skupu), paralelnost pravih u ravni,. . .

Definicija

Neka je ∼ relacija ekvivalencije skupa A i a ∈ A. Skup zove se klasa ekvivalencije elementa u odnosu na relaciju ∼.

 

 

 

Osobine klasa ekvivalencije

Teorema

Neka je ∼ relacija ekvivalencije skupa A. Tada

(1) Ca , ∅, za sve a ∈ A (tj. svaka klasa ekvivalencije je neprazan skup);

(2) a ∼ b akko Ca = Cb (tj. dva elementa imaju istu klasu ekvivalencije akko su

u relaciji)

(3) a / b akko Ca ∩ Cb = ∅; (tj. dva elementa nisu u relaciji akko su im klase disjunktne)

(4) A = ∪_a∈ACa (unija svih klasa ekvivalencije jednaka je celom skupu A.)

Primer

(1) Paralelnost pravih je relacija ekvivalencije na skupu svih pravih neke ravni α.

Klasu ekvivalencije prave p čine sve prave date ravni koje su paralelne sa p (to je, dakle, pravac prave p).

Količnički skup čine svi pravci pravih u ravni α.