Logičke operacije i iskazi
Iskazna logika ima sledeće ključne pojmove : iskaz, veznik, logička operacija, iskazna formula, tautologija..
Iskazi, veznici
Definicija : Rečenica koja ima smisla i za koju se može utvrditi da li je tačna ili netačna, naziva se iskaz.
Primer :
„Zemlja se okreće oko meseca“ – Netačan iskaz.
„2+5=7“- tačan iskaz.
„2 + 4 < 5“- netačan iskaz.
„Da li je ova rečenica iskaz?“ –nije iskaz.
Iskaze označavamo slovima p, q, r , . . . , p1, q1, . . . , p2, q2, . . . .
Od iskaza gradimo nove iskaze povezujući ih sa i, ili, nije, ako .. onda, ako i samo ako. Veze nazivamo logičkim veznicima.
Tačnost novog iskaza određujemo na osnovu tačnosti iskaza od kojih je sačinjen i značenja logičkih veznika u prirodnom jeziku.
U iskaznoj logici koriste se sledeće logičke operacije : unarne (na jednom iskazu) operacija negacije i binarne (na dva iskaza) operacije disjunkcije, konjukcije, implikacije i ekvivalencije.
Logičke operacije
Disjunkcija iskaza
Definicija: disjunkcija redom iskaza p i q je iskaz “ p ili q“ u oznaci p ∨ q, koji je tačan ako i samo ako je bar jedan od iskaza tačan.
Primer:
„2+5=7 ili 2 + 4 < 5“ – tačan iskaz.
„2+5=7 ili 2 + 4 > 5.“ – tačan iskaz.
„Šećer je slan ili slon je riba“ -netačan iskaz.
Konjukcija iskaza
Definicija: Konjukcija redom iskaza p i q je iskaz „p i q“, u oznaci p ∧ q, koji je tačan ako i samo ako su oba iskaza tačna.
Primer:
„2+5=7 и 2 + 4 < 5.“- netačan iskaz.
Implikacija iskaza
Definicija : Implikacija redom iskaza p i q je iskaz „ako p onda q“, u oznaci p ⇒ q, koji je netačan ako i samo ako je iskaz p tačan, a iskaz q netačan.
Iskaz p je pretpostavka (premisa ), a iskaz q je zaključak (konkluzija).
Primer:
„Iz 2 + 5 < 7 sledi 2 < 3“ – tačan iskaz.
„ako je 2 < 3 onda je 2+5=7“ -tačan iskaz.
„aкo je 2 < 3 onda je 2+5<7“ -netačan iskaz.
„Ako voda mrzne na 100° onda je Beč glavni grad Austrije “ – tačan iskaz
Napomena: matematičku logiku ne interesuje značenje iskaza p i q, već samo njihova istinitost. Istinitost imlikacije p ⇒ q ne zavisi od značenja iskaza p i q , već samo od njihove istinitosti .
Implikaciju p ⇒q možemo čitati na sledeći način:
„iz p sledi q“
„p povlači q“
„p implicira q“
„p je dovoljan uslov za q“
„q je potreban uslov za p“.
Primer:
Svakom od sledećih rečenica se tvrdi isto :
(1) Ako je prirodan broj deljiv sa 4 onda je deljiv i sa dva .
(2) Dovoljan uslov da prirodan broj bude deljiv sa 2 je da je on deljiv sa 4.
(3) Potrban uslov da prirodan broj bude deljiv sa 4 je da je on deljiv sa 2.
Ekvivalencija iskaza
Definicija:
Ekvivalencija redom iskaza p i q je iskaz „p ako i samo ako q“ ( p akko q), u oznaci p ⇔q, koji je tačan ako i samo ako su iskazi p i q oba tačna ili oba netačna (istih istinitosnih vrednosti).
Primer:
2 > 4 aккo 2 + 3 > 4 + 3. -tačan iskaz.
Ekvivalenciju p ⇔ q možemo čitati na sledeći način:
„p je ekvivalentno sa q“
„p je potreban i dovoljan uslov za q“
„ako p onda q i ako q onda p“.
Negacija iskaza
Definicija:
Negacija iskaza p , „nije p“, u oznaci ¬p, je iskaz koji je tačan ako i samo ako je iskaz p netačan.
Primer
„Nije 2=2“ -netačan iskaz.
Alfabet iskazne logike
Iskazna logika nastaje formalizacijom računa sa iskazima. Potrebno je odrediti skup simbola (alfabet) koji će se koristiti za građenje formula i pravila po kojima će se formirati formule.
Formule se posmatraju isključivo kao nizovi simbola, ne uzimajući u obzir bilo kakvo njihovo (moguće) značenje.
Definicija
Alfabet iskazne logike se sastoji od sledećih simbola:
skupa iskaznih slova (iskaznih promenljivih) P = {p1, p2, p3, …},
skupa logičkih veznika {∨, ∧,⇒,⇔, ¬},
skupa logičkih konstanti {⊤,⊥} ( logičke konstane mogu, ali ne moraju učestvovati u građenju formula),
skupa pomoćnih simbola {,(, ),} (zagrade).
Od ovih simbola po precizno utvrđenim pravilima grade se iskazne formule.
Iskazne formule
Definicija
Iskazne formule se definišu induktivno, na sledeći način:
- Iskazna slova i logičke konstante su iskazne formule.
- Ako su A i B iskazne formule, onda su i (A ∧ B), (A ∨ B), (A ⇒ B),(A ⇔ B) i ¬A iskazne formule.
- Iskazne formule se dobijaju samo konačnom primenom pravila (1) i(2).
Primer
Sledeći nizovi simbola su iskazne formule:
p, q, ⊤, ⊥
(p ∧ ⊤), ¬q, (⊤ ∨ ⊥),
((p ∧ ⊤) ∨ ¬q), (¬(p ∧ ⊤)), (¬q ⇔ (⊤ ∨ ⊥)).
Sledeći nizovi simbola nije iskazna formula: (p ∨ q)(⇒ p)
Konvencije
Iskazne formule označavaćemo velikim latiničnim slovima A,B,C, . . . . Zapis A = B će značiti da su formule A i B sintaksno identične (jednake kao nizovi simbola).
U svakoj formuli učestvuje samo konačno mnogo iskaznih slova.
Zapis A = A(p1, p2, . . . , pn) će značiti da su sva iskazna slova formule A u skupu {p1, p2, . . . , pn}.
Da bi se izbeglo gomilanje zagrada, po dogovoru,
- Brišemo spoljašnje zagrade,
- ako su A1, . . . ,An iskazne formule, umesto
(. . . ((A1 ∧ A2) ∧ A3) ∧ • • • ∧ An−1) ∧ An pišemo A1 ∧ A2 ∧ • • • ∧ An.
- za B važi slična konvencija,
- veznicima dajemo sledeći prioritet:
- ¬ najjače vezuje,
- ∧ i ∨ slabije vezuju,
- ⇒ i ⇔ najslabije vezuju.
Primer:
-Formulu ((¬p ∨ q) ⇒ r ) kraće zapisujemo ¬p ∨ q ⇒ r ,
-formulu ((p ⇒ ⊤) ∧ q) zapisujemo (p ⇒ ⊤) ∧ q
-p ⇒ ⊤ ∧ q znači (p ⇒ (⊤ ∧ q)).
Vrlo često ćemo prilikom dokazivanja raznih osobina formula, koristiti tzv.dokaz po složenosti iskaznih formula.
Ako treba dokazati da neka osobina O važi za sve iskazne formule, dovoljno je dokazati da tu osobinu imaju sva iskazna slova (Baza indukcije), i da iz pretpostavke da formule A i B imaju osobinu O sledi da i formule A ∧ B, A ∨ B, A ⇒ B, A ⇔ B, ¬A imaju tu osobinu (indukcijski korak).
Semantika iskazne logike
Semantički aspekt iskazne logike govori o značenju iskaznih formula.
Da bi se pravila za određivanje vrednosti iskazne formule precizno formalizovala uvodi se sledeća algebarska struktura: dvoelementni skup, čije elemente možemo označiti sa 0 i 1 ili T i F ili ⊤ i ⊥ (kao što ćemo mi učiniti) jedna unarna i četiri binarne operacija na datom skupu, koje ćemo označiti sa ¬, ∧, ∨,⇒,⇔ i koje zadajemo talicama.
Definicija
Dvoelementna algebra ({⊤,⊥}, ∧, ∨,⇒,⇔, ¬) je iskazna algebra ako su ⊤ i ⊥ dva različita znaka,
∧, ∨,⇒,⇔Binarne operacije skupa {⊤,⊥} date sledećim tablicama
Logičke operacije predstavljene istinitosnim tablicama.
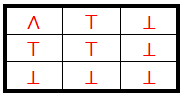
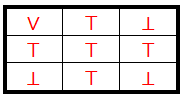
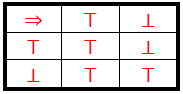
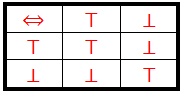
I ¬ unarna operacija skupa {⊤,⊥} tada tablicom
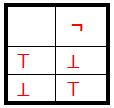
Tautologije
Definicija:
Iskazna formula koja je tačna za sve vrednosti iskaznih slova naziva se tautologija.
Važne tautologije:
(1) p ⇒p (zakon refleksije za implikaciju)
(2) p ∨ ¬p (zakon isključenja trećeg)
(3) ¬(p ∧ ¬p) (zakon neprotivrečnosti)
(4) (¬p ⇒ ⊥) ⇒p (svodjenje na apsurd)
(5) ¬¬p ⇔p (zakon dvojne negacije)
(6) p ∧ p ⇔p, p ∨ p ⇔p (zakon idempotencije)
(7) p ∨ ⊥ ⇔p, p ∨ ⊤ ⇔ ⊤
p ∧ ⊤ ⇔p, p ∧ ⊥ ⇔ ⊥
(p ⇒ ⊥) ⇔ ¬p, (⊤ ⇒ p) ⇔p
(8) p ∧ q ⇔q ∧ p, p ∨ q ⇔q ∨ p (zakoni komutacije)
(9) p ∧ (p ⇒q) ⇒ q (MP-modus ponens)
(10 ((p ⇒q) ∧ ¬q) ⇒ ¬p (MT-modus tollens)
(11) ((p ⇒q) ⇒p) ⇒ p (Pirsov zakon)
(12) p ∧ (p ∨ q) ⇔p, p ∨ (p ∧ q) ⇔p (zakoni apsopcije)
(13) (p ⇒q) ⇔ (¬q ⇒ ¬p) (zakon kontrapozicije)
(14) ¬(p ∧ q) ⇔ ¬p ∨ ¬q,¬(p ∨ q) ⇔ ¬p ∧ ¬q (De Morganovi zakoni)
(15) (p ⇒q) ⇔ ¬p ∨ q (zakon uklanjanja implikacije)
(16) (p ⇔q) ⇔ (p ⇒q) ∧ (q ⇒p) (zakon uklanjanja ekvivalencije)
(17) p ∧ (q ∧ r ) ⇔ (p ∧ q) ∧ r ,p ∨ (q ∨ r ) ⇔ (p ∨ q) ∨ r (zakoni asocijacije)
(18) p ∧ (q ∨ r ) ⇔ (p ∧ q) ∨ (p ∧ r ),
p ∨ (q ∧ r ) ⇔ (p ∨ q) ∧ (p ∨ r ) (zakoni distribucije)
(19) ((p ⇒ q) ∧ (q ⇒ r )) ⇒ (p ⇒ r ) (tranzitivnost implikacije)
(20)((p ⇔ q) ∧ (q ⇔r ) )⇒ (p ⇔ r ) (tranzitivnost ekvivalencije)
Tablični metod
Istinitosna vrednost date iskazne formule zavisi samo od vrednosti iskaznih slova koja u njoj učestvuju.
Za formulu A(p1, . . . , pn) (sa n iskaznih slova) ima 2n različitih „kombinacija“ vrednosti iskaznih slova.
Ovaj postupak se sastoji u proveri istinitosne vrednosti formule u svih 2n slučajeva, što se prikazuje tablicom.
Primer
Iz tablice istinitosti za formulu A = (p ⇒q) ⇔ ¬p ∨ q
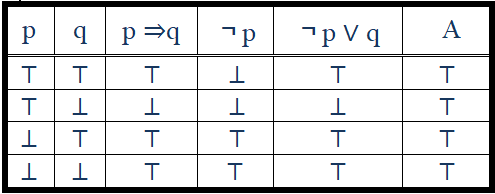
zaključujemo da je ova formula tautologija.
Zaglavlje tablice formiramo tako što najpre unesemo sva iskazna slova (u ovom sličaju p i q), a zatim postavljamo manje celine za koje možemo utvrditi istinitost. Koristimo tablice (definicije) odgovarajućih logičkih operacija.
Centralna operacija ove formule je ekvivalencija. Leva strana fomule je p⇒q ( iskazi su postavljeni u tablici ) i možemo utvrditi tačnost ove implikacija. Nju unosimo u zaglavlje tablice. Desna strana formule je ¬p∨q . Za navedenu disjunkciju ne možemo utvrditi tačnost jer nije određena tačnost ¬p. Iz tog razloga najpre pišemo ¬p, a zatim ¬p∨q . Kada odredimo istinitosnu vrednost leve i desne strane ispituje se centralna operacija ⇔.
Broj redova u tablici izračunava se kao 2n, gde je n broj iskaznih slova u formuli. u našem slučaju 22 =4.
Istinitosnu vrednost iskaza postavljamo tako da pokrijemo sve moguće rasporede ( za prvi iskaz dva tačna, dva netačna, a za drugi naizmenično tačno netačno).
Za formule sa 3 iskazna slova broj redova je 8 (postavljamo za prvi iskaz 4 tačna, četiri netačna,za drugi iskaz dva tačna, dva netačna…, a za treći naizmenično tačno netačno…)
Rešeni zadaci
Primeri
Dati su iskazi p i q. Naći vrednost formule F ako je a) F: (p∧¬q)⇔p ; b)F:(¬p∨q)⇒(p∧q) a za iskaze p i q važi
Najpre određujemo istinitosnu vrednost iskaza p . Sređujemo levu i desnu stranu i utvrđujemo da li su jednake. Ako jesu potvrđena je tačnost iskaza i njegova istinitosna vrednost je T a ako nisu tada je istinitosna vrednst ⊥ .
τ(p)=Τ ili τ(p)=⊥ (tau od r)
V(p)=T ili V(q)=⊥
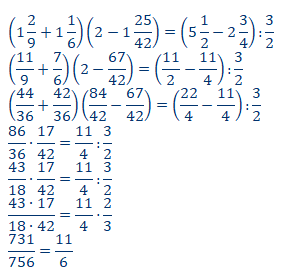
Mešovite brojeve prevodimo u razlomke.
Određujemo NZS .
Izvršavamo naznačene operacije .
Leva strana iskaza nije jednaka desnoj.
Zaključujemo da je iskaz netačan. V(p)=⊥
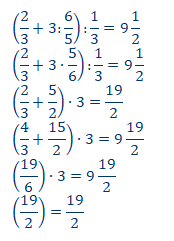
Postupak ponavljamo za iskz q.
Leva strana iskaza jednaka je desnoj, pa zaključujemo da je istinitasna vrednost iskaza je T .
V(q)=T.
a) U formuli (p∧¬q)⇔p menjamo iskazna slova sa njihovom istinitosnom vrednošću
(⊥∧¬T)⇔⊥ ,primenom definicije logičke operacije negacija ¬T=⊥
(⊥∧⊥)⇔⊥ ,primenom definicije logičke operacije konjukcija ⊥∧⊥=⊥
⊥⇔⊥ ,slično rešavamo ekvivalenciju
T , za date iskaze formula je tačna
b) U formuli (¬p∨q)⇒(p∧q) menjamo iiskazna slova istinitosnom vrednošću tih iskaza.
(¬⊥∨T)⇒(⊥∧T) ,rešavamo negaciju
(T∨T)⇒(⊥∧T) ,rešavamo disjunkciju i konjikciju
T⇒⊥ ,rešavamo implikaciju
⊥ ,zaključujemo za date iskaze formule nije tačna.
Ispitati da li su sledeće formule tautologije :
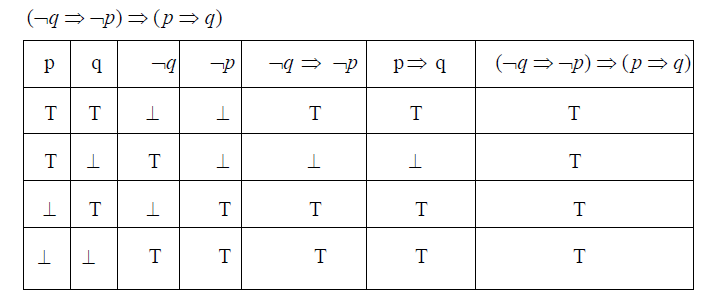
I) (¬q⇒¬p)⇒(p⇒q)
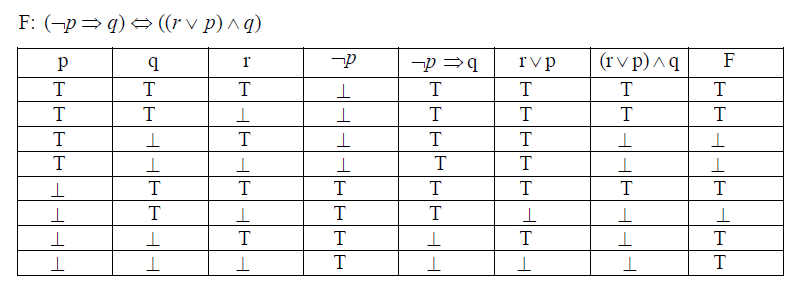
II) (¬p⇒q)⇔((r∨p)∧q