Granična vrednost niza
Jedna od centralnih problema koji se postavljeju za niz an=(a1,a2,… )jeste pitanje šta se dešava sa opštim članom an niza kada n postaje sve veće i veće (kada n neograničeno raste).
Posmatrajmo niz čiji je opšti član an=1/n
Jasno je: štoj je n veći broj , opšti član ovog niza postaje sve manji i sve se više približava broju 0 ali ni za jedan prirodan broj n neće biti jednk 0.
Iako 1/n nikad nije 0 , što je n veće i veće, an je sve bliže broju 0. Zbog toga kažemo da je 0 granična vrednost (limes) i pišemo:
![]()
U geometrijskoj interpretaciji, ako predstavimo članove niza na brojnoj pravoj vidimo da se članovi niza nagomilavaju oko tačke 0. Ako oko tačke 0 opišemo neki interval male dužine videćemo da će samo konačno mnogo članova niza ležati izvan tog intervala, dok će beskonačno mnogo članova niza biti u intervalu.
Graničnu vrednost možemo definisati i definicijama koje slede
1.Neka je n0 fiksiran prirodan broj. Ako svi članovi niza an imaju osobinu S , osim možda prvih n0 članova niza tada kažemo da skoro svi članovi niza an imaju osobinu S.
2.Neka je n0 fiksiran prirodan broj. Ako svi članovi niza an počev od člana ano+1 pa nadalje, tj ako svi članovi an za n=no+1, no+2,…imaju osobinu S, onda kažemo da skoro svi članovi niza imaju osobinu S
Neka je a realan broj i neka je ε>0. Interval (a-ε, a+ε) naziva se ε-okolina broj a.
Preciznija definicija granične vrednosti niza je :
Realan broj a je granična vrednost niza an ako se u proizvoljnoj ε okolini broja a nalaze skoro svi članovi niza an.
Ako takav broj a postoji, onda se kaže da je niz an konvergentan i da kovergira broju a i piše se
![]()
Ako ne postoji realan broj a takav da se u svakoj e okolini tog broja nalaze skoro svi članovi niza an onda se kaže da niz an nije kovergentan ili da je divergentan i pišemo
![]()
Neka svojstva knvergentnih nizova

Zadatak :
Odredi sledeće granične vrednosti :
Primer a)
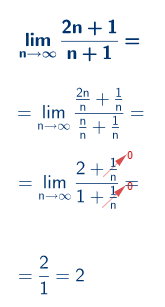
Rešavamo neodređenost (∝ /∝). Limes razlomka u kome se nalazi n u imeniocu i broiocu određujemo tako što svaki član razlomka delomo sa n najvećeg stepena.
U ovom slučaju sa n.
Svaki razlomak sređujemo (kratimo).
Svaki član koji je posle sređivanja ostao kao razlomak sa n ( bez obzira na stepen) u imeniocu teži nuli jer mu imenilac teži beskonačnosti.
Kada dobijemo kostantu limes- granična vrednost je određena.
Primer b)
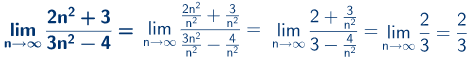
Primer c)
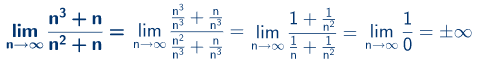
Primer d)
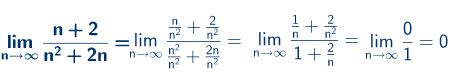
Primer e)
Rešavamo neodređenost ∞ – ∞
Dati izraz proširićemo tako da dobijemo u broioci razliku kvadrata.
Pod korenom dobijamo kvadrat binoma. Posle skraćivanja korena i kvadrata ostaje apsolutna vrednost. Ako analiziramo znak izraza n2-10n , uviđamo da je pozitivan za n>10. Kako n teži beskonačnosti to možemo bez gubitka opštosi da se oslobodimo apsolutne vrednosti.
Sada imamo razlomak sa n u imeniocu i broiocu pa ćemo deliti svaki član razlomka sa n, jer je to najveći stepen.
Naravno, nećemo zaboraviti da deljenjem sa n kod potkorenog izraza, delimo sa n2.
.
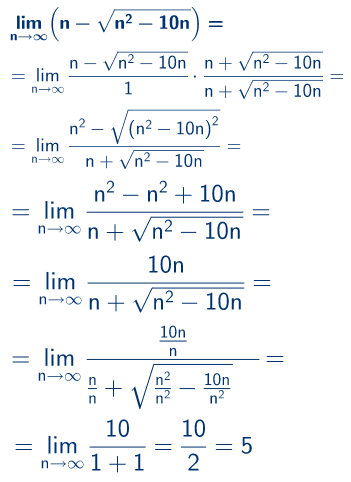
Primer f)
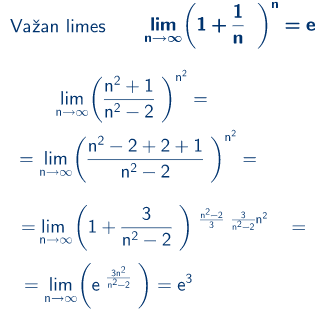
Rešavamo neodređenost
![]()
Izraz u zagradi moramo da transformišemo tako da bude sličan izrazu u navedenom važnom limesu. Uočavamo da je razlomak u zagradi recipročna vrednost izložioca.
Kako je prvi sabirak u datoj formuu 1 to znači da treba izraz u našem primeru da podelimo na dva razlomka. Da bijedan od razlomaka dao 1 treba da ima jednak imenilac i brilac. Zato broilac dopunimo sa -2+2.
Izaz koji dobijamo u zagradi ima jedinici kao prvi sabirak ali drugi sabirak nije recipročna vrednost izložioca kao u formuli. Izložilac proširimo sa 1 , odnosno prizvodom recipročnom vrednošći drugog sabirka i drugog sabirka (to je uvek 1).
Problem smo sveli na određivanje limesa izložioca .
