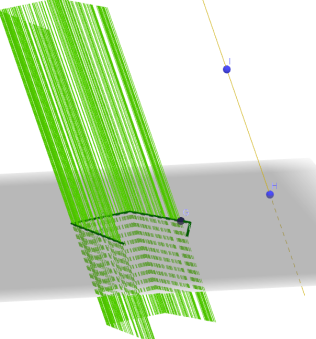
Prizma i prizmatična površ
Definicija: Neka je data jedna izlomljena linija (vodilja- generatrisa) u nekoj ravni α i prava p koja je van ravni α i nije joj paralelna. Unija svih pravih paralelnih (direktrisa) pravoj p koje seku datu izlomljenu liniju, naziva se n-tostranom prizmatičnim površi.
Ako je vodilja prizmatične površi zatvorena izlomljena linija , tada se ta prizmatična površ je zatvorena.
Definicija Neka je data jedna n-tostrana prizmatična površ i dve međusobno paralelne ravni α i β koje nisu paralelne izvodnicama te prizmatične površi. Skup svih tačaka koje leže, istovremeno, u unutrašnjoj oblasti date prizmatične površi ili na njoj i između ravni α i β ili u nekoj od njih, naziva se n-tostrana prizma
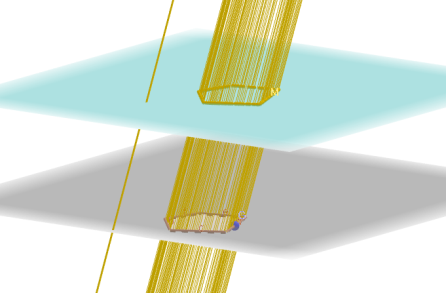
Ako su bočne ivice prizme normalne na ravni osnova, tada kažemo da je to prava prizma, a u suprotnom slučaju nazivamo je kosom prizmom.
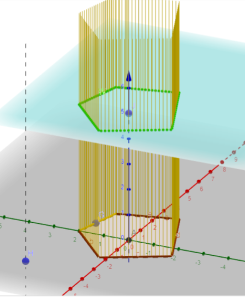
Animacija -Generisanje prizmatične površi i prizme
Kako se prizme sastoji od dve podudarne osnove i omotača, to je površina prizme zbir dvostruke površine osnove i površine omotača, pri čemu se pod površinom omotača podrazumeva zbir površina svih bočnih strana prizme . Ako je prizma prava u omotaču su pravougaonici, a ako je kosa, paralelogrami. Ako površinu prizme obeležimo sa P, površinu njene osnove sa B, a površinu omotača sa M, tada je P=2B+M. Obrazac za izračunavanje zapremine prizme je V=BH.
Prizma i ravan -preseci
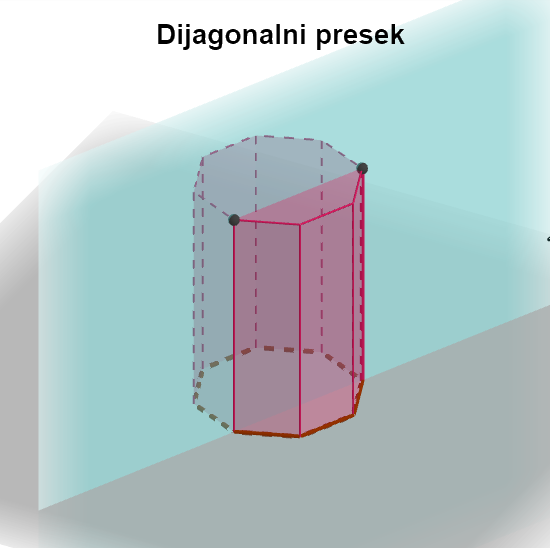
Presek prizme i ravni koji sadrži dijagonale osnova prizme naziva se dijagonalni presek.
Prizma i ravn – presek koji paralelan sa osnovom prizme
Presek prizme i ravni koja je paralelna bazi n-tostrane prizme je n-tostrani mnogougao čija je površina jednaka je površini baze.
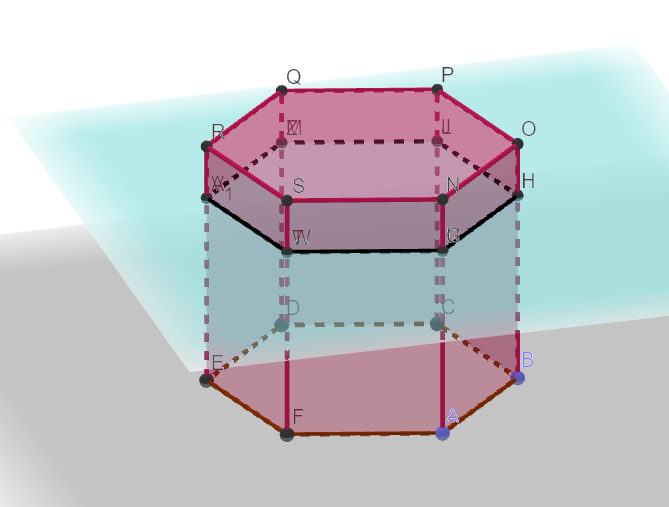
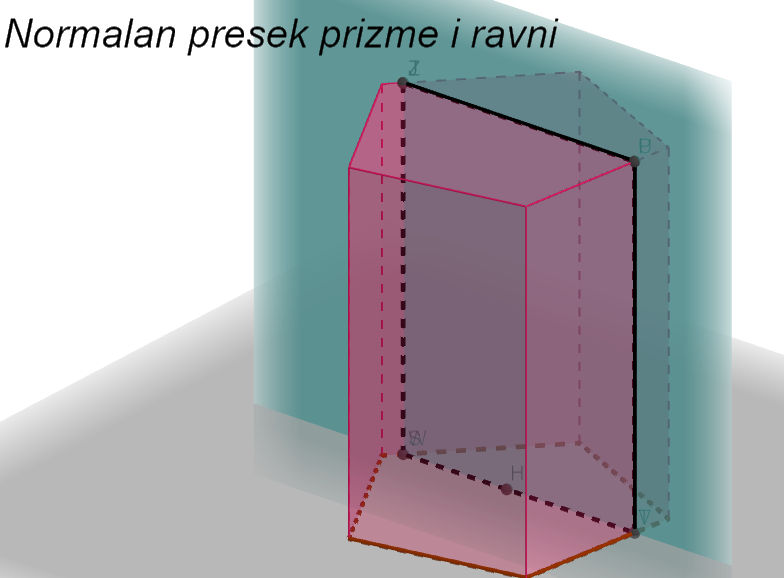
Prizma i ravn koja je paralelna bočnim ivicama prizme- presek
Presek ravni koja je paralelna ivicama prize može biti duž ako ravan sadrži jednu ivicu, četvorougao ako ravan seče dve stranice osnove prizme.
Ako je prizma prava tada presek može biti pravougaonik ili duž.
Ako ravan sadrži dijagonalu osnove prizme tada je presek dijagonalan.
Animacija-Presek ravni koja je paralelna ivicama prizme i ravni
Prizma i ravn koja nije paralelna osnovi prizme ni bočnim ivicama prizme-presek
Presek ravni i prizme određen je uglom koji ravan zaklapa sa ravni osnove. Da bi došli do površine tog preseka razmotićemo najpre normalnu prijekciju na ravan α.
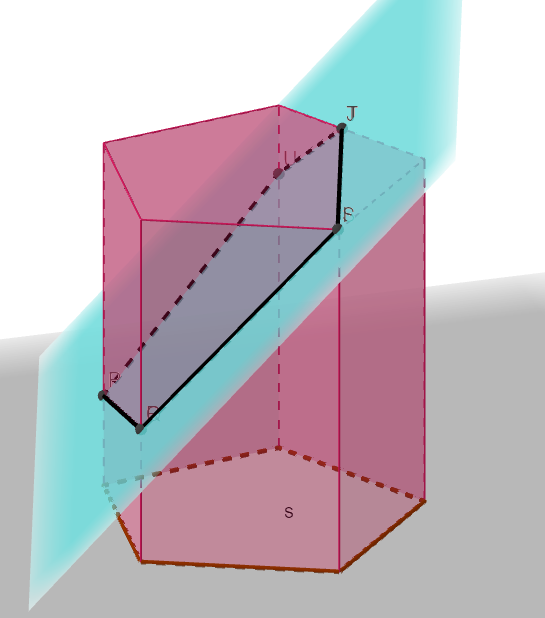
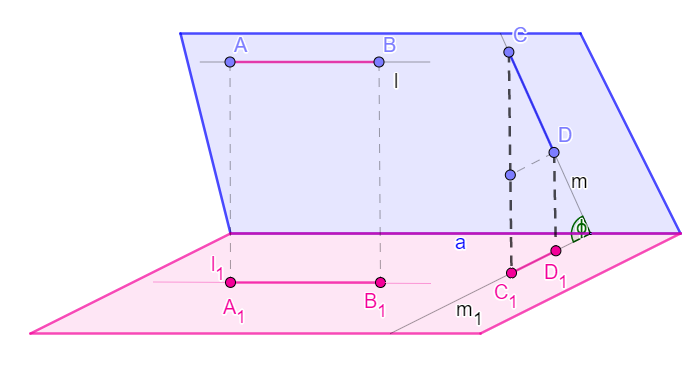
Posvršina kosog preseka
Neka je α∩π=a,∠(α,π)= φ -oštar ugao . Neka prava l ∈π i neka je l || a. Normalno projektovanje održava paralelnost pravih. Ako je prajekcija prave l prava l1 i prajekcija prave a prava a, tada je l || a || l1.
Duž AB prave l projektuje se u duž A1 B1 prave l1 i za njih važi AB≅ A1 B1.
Posmatrajmo sada pravu m koja je normalna na pravu a i njenu projekciju m1 koja je takođe normalna na a. Ugao φ je ugao između m i m1. Možemo zaključiti da je C1D1=CDcosφ. Slično dolazimo do zaključka P1=Pcosφ
Vežba
