POLIEDRI
Kako nastaju poliedri ? Kako se definišu poliedri?
Skup površi mnogouglova takvih da je svaka stranica svakog mnogougla ujedno i stranica još samo jednog mnogougla, obrazuju zatvorenu površ koja se naziva poliedarska površ. Deo geometrijskog prostora koji ograničava (zatvorena) poliedarska površ je unutrašnjost poliedarske površi. Unija poliedarske površi i njene unutrašnjosti je poliedar.
Površi mnogouglova, nazivaju se strane (ili pljosni) poliedra, a stranice tih mnogouglova nazivaju se ivice poliedarske površi i poliedra. Rogljevi koje obrazuju strane poliedra sa jednim zajedničkim temenom su rogljevi poliedra, a vrhovi tih rogljeva su temena poliedra.
Svaka duž koja spaja dva temena poliedra a ne pripada ni jednoj strani poliedra predstavlja dijagonalu poliedra. Svaka ravan koju određuju tri temena poliedra i ne sadrži nijednu stranu poliedra predstavlja dijagonalnu ravan poliedra.
Poliedar dobija naziv prema broju strana. Tetraedar-4 strane heksaedar-6 strana oktaedar-8 strana dodekaedar-12 strana ikosaedar- 20 strana
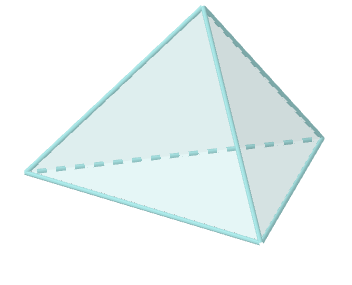
Tetraedar
Površi: 4 jednakostraničnih trouglova
Broj ivica:6
Broj temena: 4
Broj ivica u jednom temanu :3
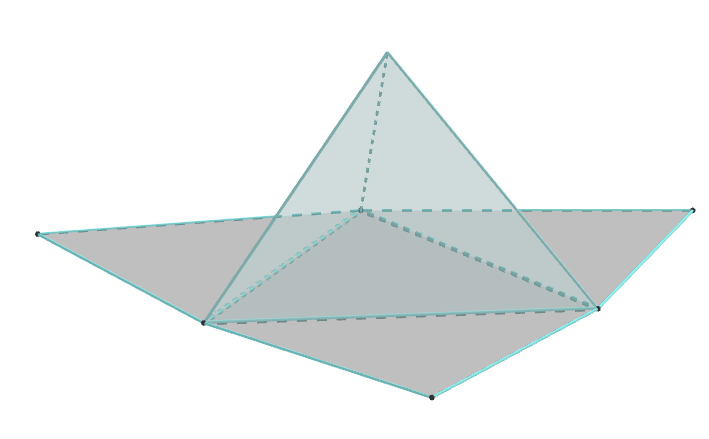
Heksaedar
Površi: 6 kvadrata
Broj ivica:12
Broj temena: 8
Broj ivica u jednom temanu :3

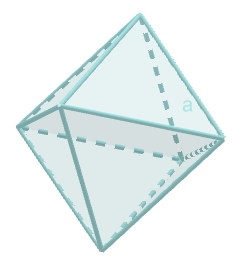
Oktaedar
Površi: 8 jednakostraničnih trouglova
Broj ivica:12
Broj temena: 6
Broj ivica u jednom temanu :4
Animacija: Oktaedar i njegova mreža
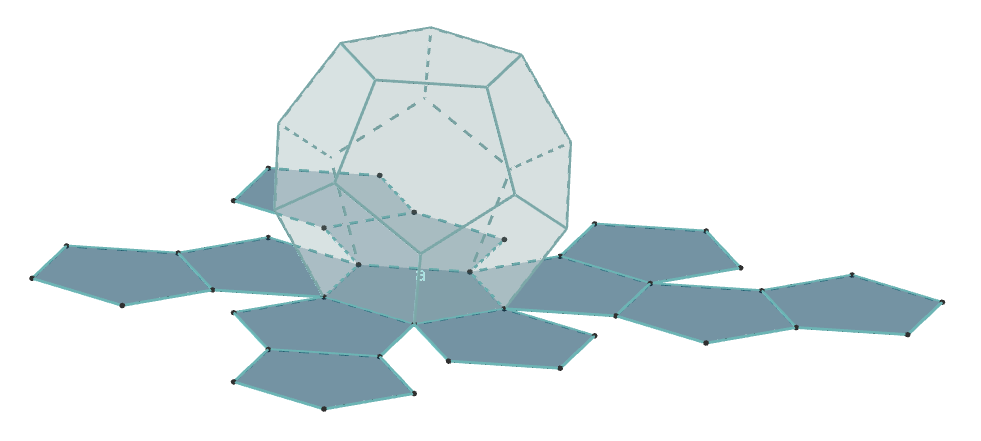
Dodekaedar
Površi: 12 pravilnih petouglova
Broj ivica:30
Broj temena: 20
Broj ivica u jednom temanu :3
Animacija : Mreža dodekaedra
Ikosaedar
Površi: 20 jednakostraničnih trouglova
Broj ivica:30
Broj temena: 12
Broj ivica u jednom temanu :5
Anaimacija : Ikosaedar
Poliedri mogu biti konveksni i nekonveksni-konkavni. Poliedar je konveksan ukoliko svaka duž koja spaja njegove dve proizvoljne tačke pripada tom poliedru, u suprotnom slučaju poliedar je nekonveksan odnosno konkavan.
Poliedari čije su sve strane regularni podudarni mnogouglovi i čiji su svi rogljevi podudarni naziva se pravilni poliedri.
Konveksni pravilni poliedri nazivaju se Platonova tela.
Karakteristike poliedara:
- n – broj temena (страница) strana poliedra
- k – broj strana koje čine jedan rogalj
- T – broj temena poliedra
- S – broj strana poliedra
- I – broj ivica poliedra
