Valjak ima oblika kakav srećemo svakodnevno. Na primer, razne vrste metalnih cevi, konzervi, razne vrste posuđa, itd. Poznavanje površina takvih tela značajno je za njihovu izradu i primenu.
Neka je u ravni π data kružnica L (direktrisa, vodilja) i prava a koja sa ravni π ima samo jednu zajedničku tačku (generatrisa, izvodnica). Skup tačaka svih pravih u prostoru koje su paralelne pravoj a i sadrže tačke krive L, obrazuju površ koju nazivamo kružna cilindrična površ.
Ako napravimo preseke takve površi dvema ravnima, paralelnim ravni direktrise, dobićemo u preseku dve kružnice L1 i L2 podudarne kružnici L. Telo ograničeno delom cilindrične površi i između paralelnih krugovima L1 i L2 naziva se valjak. Ukoliko je generatrisa a normalna na ravan direktrise L takav valjak nazivamo pravim valjkom, a ako nije kosim.
Kako se pravi valjak sastoji iz dva podudarna kruga i omotača, to je za dobijanje površine valjka potrebno izračunati njihove površine . Obeležimo sa B površinu jedne osnove valjka, B=π⋅r². Omotač valjka čini paralelogram čije su stranice 2rπ i H, pa je površina omotača M=2rπH. I sada je jasno da je površina valjka
P=2B+M= 2πr²+2πrH= 2πr(r+H).
Zapremina valjka je V=BH ili V=r²πH
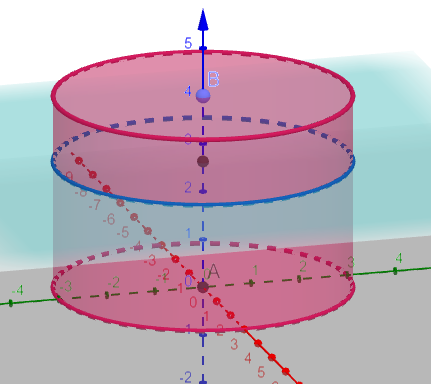
Presek valjka i ravni paralelne osnovi valjka
Presek ravni kaja je paralelna osnovama valjka naziva se paralelan presek . Presek je podudaran krugu u bazama valjka.
Animacija : Valjak i ravan -paralelan presek
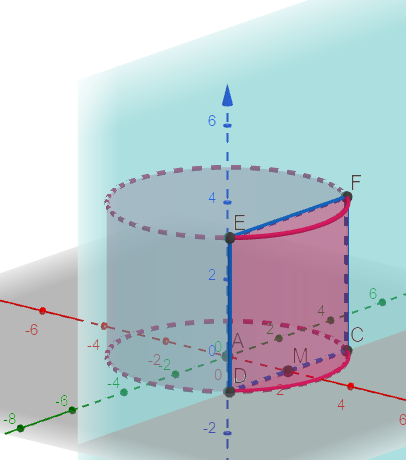
Presek valjka i ravni koja je paralelna izvodinici valjka
Presek ravni koja je paralelna izvodnici valjka je četvorougao ili duž ako je presek ravani i osnove prava koja je tangenta na krug u osnovi .
Ako je valjak prav presek je duž ili provougaonik. Ako sadrži osu valjka neziva se osni presek .
Animacija : Valjak i ravan -normalan presek
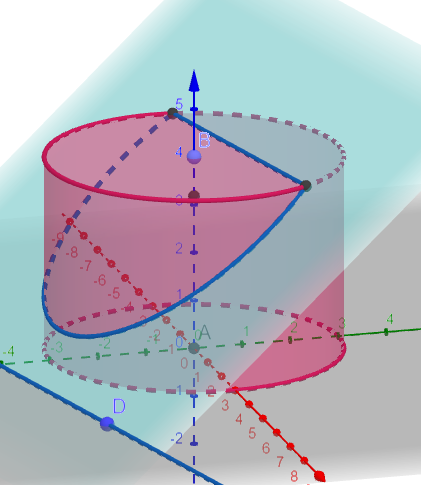
Presek valjka i ravni koja nije ni paralelna ni normalna na ravna osnove
Ravan koja nije paralelna ni osnovi ni izvodnicama valjka, sa valjkom gradi kos presek.
Presek može biti tačka, elipsa, unija parabole i duži…
Animacija : Valjak i ravan -kos presek