Kvadratni koren je unarna matematička operacija inverzna kvadriranju. Oznaka ove operacije nad nekim brojem x je , i čita se kao „koren iz x“.
Potpuno ispravno bi bilo da pišemo i izgovaramo, „kvadratni koren od x“.
![{displaystyle {sqrt[{2}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6de2cdac50381036216dfd74be1e6e2303d5dc7a)
Kvadratni koren broja x je nenegativan broj koji pomnožen sam sobom daje x.
Za svaki pozitivan broj x postoje tačno tačno dva realna broja čiji su kvadrati jednaki broju x. Jedan od tih brojeva je pozitivan a drugi negativan.
Koren iz 0 jednak je 0.
Kubni koren broja x je broj čiji je kub jednak broju x.
Na sličan način se definiše i n-ti koren
Zadatak 1:
Zadatak 2: Uprosti izraz
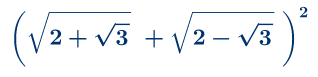
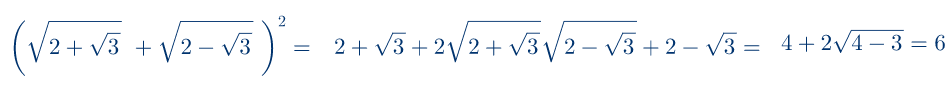
Zadatak 3:Uprosti izraz:
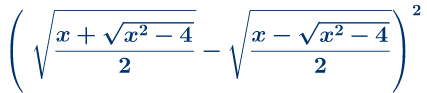
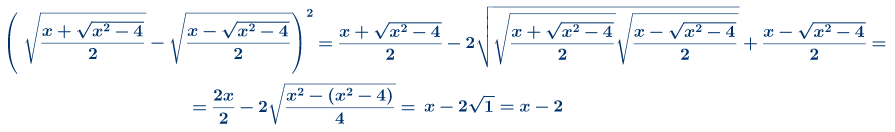
Zadatak 4: Izračunaj
Zadatak 5: Uprosti izraze
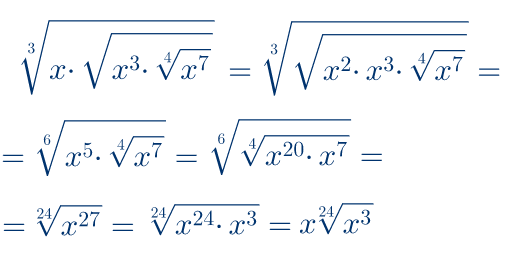
ili
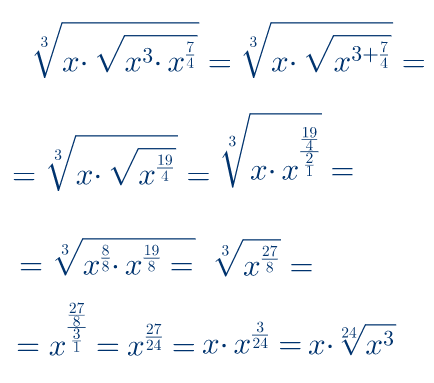
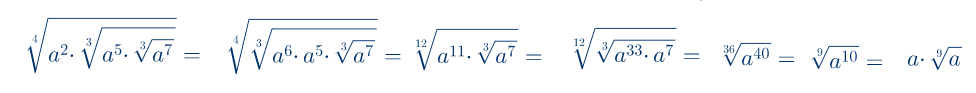
Zadatak 6: Izračunati
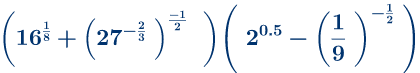
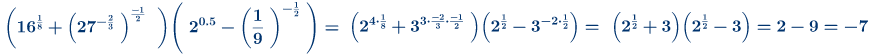
Zadatak 7: Izračunati
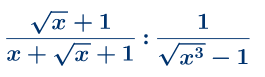
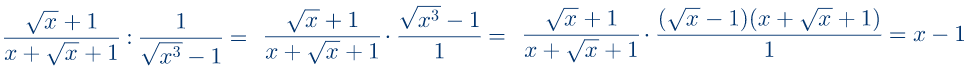
Stepen čiji je izvožilac racionalan broj